|
« Modelling frames using two-dimensional finite elements
The frame function in regions of columns »
|
Modelling slabs using bar and two-dimensional finite elements Finite element method assists in defining slabs functionality with significant accuracy. However, in order for the result to represent the reality, suitable assumptions should be adopted. The effects of the following factors are examined thoroughly in Annex A: 1) The frame function of slabs at the areas near columns 2) The vertical displacement of beams 3) The torsional stiffness of beams The above factors affect the behavior of slabs. In order to investigate this effect, a simple structure is being modelled in two ways: (i) Using bar finite elements, according to which the slab is modeled as a grid of main and secondary joists, without the assumption of rigid bodies. (ii) Using two-dimensional triangular finite elements. The summary of Annex A is presented below: 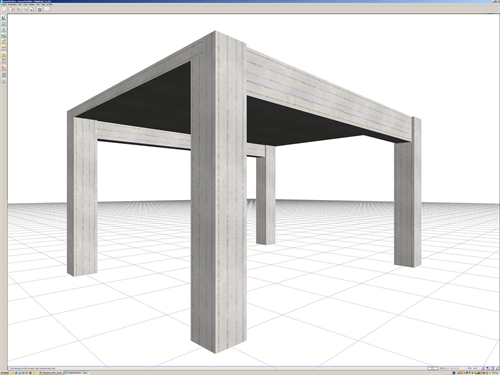 Figure 3.3.6-1: The structure of project <B_331> of the related software (columns sections 400/400, beams sections 300/500, slab thickness 170 mm)
Figure 3.3.6-1: The structure of project <B_331> of the related software (columns sections 400/400, beams sections 300/500, slab thickness 170 mm) Figure 3.3.6-1: The structure of project <B_331> of the related software (columns sections 400/400, beams sections 300/500, slab thickness 170 mm) 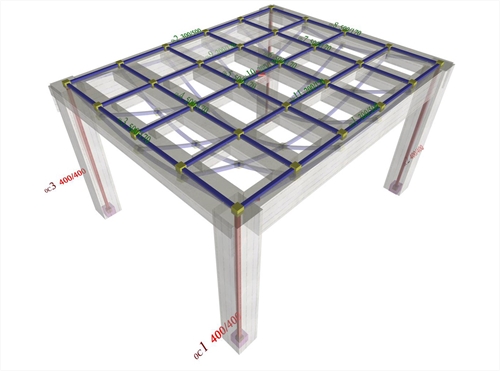 Figure 3.3.6-2: Slab modelled with bar finite elements and the displaced structure (project <B_336>)
Figure 3.3.6-2: Slab modelled with bar finite elements and the displaced structure (project <B_336>) Figure 3.3.6-2: Slab modelled with bar finite elements and the displaced structure (project <B_336>) 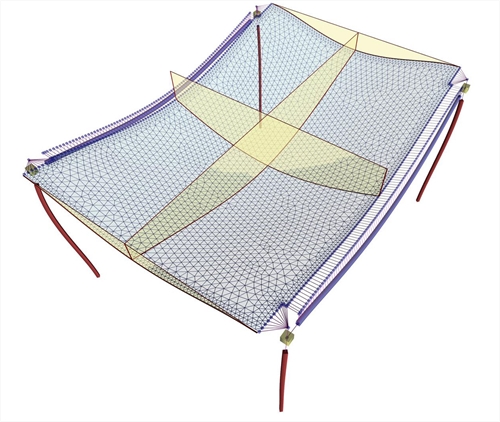 Figure 3.3.6-3: Slab modelled with triangular finite elements (project <B_336>) (a=beam-slab common deflection curve)
Figure 3.3.6-3: Slab modelled with triangular finite elements (project <B_336>) (a=beam-slab common deflection curve) Figure 3.3.6-3: Slab modelled with triangular finite elements (project <B_336>) (a=beam-slab common deflection curve)
|
« Modelling frames using two-dimensional finite elements
The frame function in regions of columns »
|

|