STIFFNESS OF MULTISTOREY PLANE FRAMES Β.1 Stiffness of frame crossbar The assessment of the behaviour of the one-storey plane frame under horizontal seismic forces was demonstrated in §5.1. The behaviour of each frame column was explained, stiffness being the basic quantity measuring its structural behaviour. What most mattered was the relation between the column stiffnesses. In multistorey plane frames, the quantity measuring the behaviour under horizontal seismic forces is the crossbar stiffness. Crossbar is the horizontal part of a frame connecting columns. The crossbar is either usually a flanged beam or a slab strip. In case crossbars 4 and 5 of the frame illustrated below were connected through a slab, then they would both constitute one single crossbar (i.e. in this case the concept of the crossbar would be equivalent to the concept of the diaphragm). 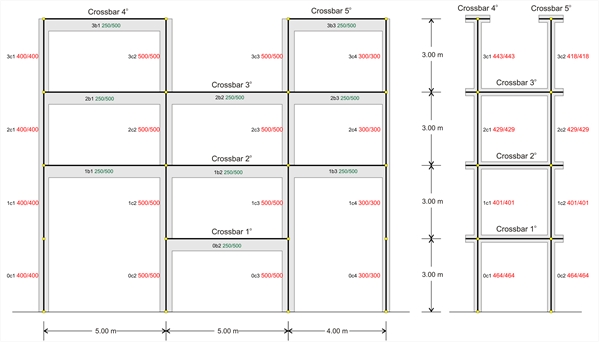 Figure B.1-1: Common practice frame and equivalent system
Figure B.1-1: Common practice frame and equivalent system Figure B.1-1: Common practice frame and equivalent system
Figure B.1-1: Common practice frame and equivalent system Stiffness Ki , of crossbar i, of a plane frame is the ratio of the horizontal seismic force H acting on the crossbar, parallel to the plane of the frame, to the corresponding crossbar displacement δi, i.e. Ki=H/δi. To compare the interstorey stiffnesses, it is very helpful to use a simpler frame type structure, with the same behaviour as the actual frame under horizontal seismic forces. Stiffness calculation of crossbar i | |
Figure B.1-3: Common Practice Frame
Frame analysis results,
crossbar displacements δi and column shear forces
(Stiffness of crossbar i: Ki=H/δi) Example project <B_b1-1>:
for Η=100 kN and i=2, δ2=2.589 mm à
K2=H/δ2=100·103N/(2.589·10-3m)=38.6·106 N/m | Figure B.1-4: Equivalent System
The analysis gives the same displacements, thus the same stiffness for crossbar i Example project < B_b1-2>:
for Η=100 kN, δ2=2.589 mm àK2=38.6·106 N/m | Notes:  Figure B.1-5
Figure B.1-5 Figure B.1-5 - In general the crossbar joint displacements slightly differ between them, due to axial forces. However crossbars are usually connected with slabs forming not only strong flanged beams, but also horizontal diaphragms assumed axially non deformable.
- All floor joints develop significant displacements. Also, shear forces are developed in all columns and beams. The shear forces, however, of the crossbars, above crossbar i, are very small.
- The analyses both of the actual and the idealised frames are performed based on these assumptions:
Β.2 Equivalent multistorey frame – crossbar relative stiffness The equivalent frame may comprise one, two, or more vertical columns and should result in the same displacements as the actual frame. It is easier to perceive this equivalence using an one-bay frame composed of equivalent fixed-ended columns and eventual segmented crossbars. The stiffness of the idealised columns at each crossbar is calculated for each floor separately and their sum should be equal to that of the actual crossbar of the floor considered. To this end, the relative stiffness of floor crossbar is defined . The idealised system of the present paragraph example comprises one crossbar at each of the first three floors and two distinct fixed-ended columns at the fourth floor. The sum of stiffnesses of the two idealised columns of the first three levels is equal to the sum of stiffnesses of the four columns of the actual frame. At the fourth level, the left idealised column corresponds to the left two-column crossbar of the actual frame while the right idealised column corresponds to the right two-column crossbar of the actual frame. Relative stiffness KRi , of crossbar i, of a multistorey plane frame is the ratio of the horizontal seismic force Η acting on crossbar i, to the relative displacement between the crossbar i and the underlyingcrossbar i-1, when identical force Η acts on the latter, i.e. KRi=H/(δi-δ i-1). Relative stiffness calculation of crossbar i
Example project < B_b1-1> |  Figure B.2-1: Analysis of crossbar iunder horizontal force HExample: for Η=100 kN and i=2, δ2=2.589 mm
Figure B.2-1: Analysis of crossbar iunder horizontal force HExample: for Η=100 kN and i=2, δ2=2.589 mm Figure B.2-1: Analysis of crossbar iunder horizontal force HExample: for Η=100 kN and i=2, δ2=2.589 mm | 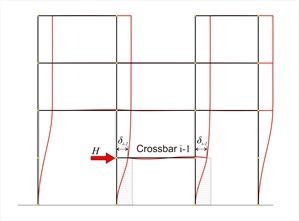 Figure B.2-2: Analysis of crossbar i-1under horizontal force HExample: for Η=100 kN and i-1=1, δ1=0.936mm
Figure B.2-2: Analysis of crossbar i-1under horizontal force HExample: for Η=100 kN and i-1=1, δ1=0.936mm Figure B.2-2: Analysis of crossbar i-1under horizontal force HExample: for Η=100 kN and i-1=1, δ1=0.936mm | | Example: for Η =100 kN and
i=2, δ 2 =2.589 mm | Example: for Η =100 kN and
i-1=1, δ 1 =0.936mm | Example: ΚΖ ,2 =100.00 ·103N/[(2.589-0.936)·10-3m=60.5 N/m | | | Note : In the special case of i=1, KΖ,1=K1=100.00·103N/(0.936·10-3m)=106.8 N/m, i.e. at the first level, the relative and the absolute stiffnesses coincide. The stiffnesses derived from the application of the above definitions depend only on the geometry of the frame and not on the magnitude of the loading, i.e. a loading of double magnitude results in double displacements but the stiffness remains the same. The stiffnesses Κi and the relative stiffnesses ΚZi of all crossbars are calculated tabulating the above procedure, | Crossbar i | δo,i | Κi | δi-δi-1 | ΚZi | Equivalent
cross-sections | | | Mm | ·106 N/m | mm | ·106 N/m | mm/mm | | 5 | 6.6789 | 14.97 | 2.810(*) | 35.59 | 418/418 | | 4 | 6.1173 | 16.35 | 2.248 | 44.48 | 443/443 | | 3 | 3.869 | 25.85 | 1.280 | 78.13 | 429/429 | | 2 | 2.589 | 38.62 | 1.653 | 60.50 | 401/401 | | 1 | 0.936 | 106.84 | 0.936 | 106.84 | 464/464 | (*) Here, the underlying crossbar is No 3, not No 4 Β.3 Relative stiffness of crossbar column For the sake of generality of the method as well as for the comparison with the one-storey frames of §5.1, the term relative stiffness of a crossbar column is also defined. Relative stiffness of crossbar column of multistorey plane frame is the ratio of its shear force to the force H multiplied by the relative crossbar stiffness KRi. The shear forces Vi,j carried by the column j of level i and
the corresponding relative stiffnesses ΚZi,j | Crossbar i | ΚZ | Vi,1 | ΚZi,1 | Vi,2 | ΚZi,2 | Vi,3 | ΚZi,3 | Vi,4 | ΚZi,4 | Σ(Vi) | | | ·106 N/m | kN | ·106N/m | kN | ·106N/m | kN | ·106N/m | kN | ·106N/m | | | 5 | 35.59 | - | - | - | - | 75.8 | 27.0 | 24.2 | 8.6 | 100.00 | | 4 | 44.48 | 38.8 | 17.3 | 61.2 | 27.2 | - | - | - | - | 100.00 | | 3 | 78.13 | 18.6 | 14.5 | 36.6 | 28.6 | 34.9 | 27,3 | 9.9 | 7.7 | 100.00 | | 2 | 60.50 | 9.0 | 5.4 | 44.2 | 26.7 | 43.6 | 26.4 | 3.2 | 1.9 | 100.00 | | 1 | 106.84 | 4.0 | 4.3 | 47.3 | 50.5 | 47.3 | 50.5 | 1.4 | 1.5 | 100.00 | Important: The examination of the behaviour of multistorey frames, beyond its educational purpose is also the basis of the assessment of the multistorey space frames, which function along both plane frame directions x and y. Of course, the rotation factor, considered in Appendix D, is also involved in the space frame analysis. Β.4 Effect of slabs on stiffnesses using finite elements Indicatively a four-storey frame of 3.0 m high columns is analysed. Each floor comprises columns of 400/400 cross-section, beams of 6.0 m span and 300/500 cross-section and slabs of 150 mm thickness and 1.0 m width at each side of beam faces. Two analyses are performed: First analysis : a plane frame is analysed, where the influence of slabs is accounted for assuming the effective flange width in accordance with EC2. In frame analysis, beams and columns are usually modelled with members. The influence of slabs is taken into account by adding a beff wide flange to the rectangular beam, and a flanged beam is formed, usually of T section. 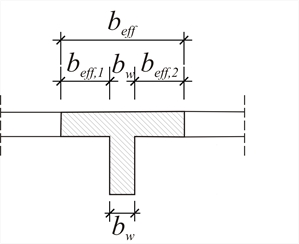 Figure B.4-1
Figure B.4-1 Figure B.4-1
The width b eff is called effective width and conventional values are ascribed to it. The effective width magnitude, as shown in §3.1.2, depends on certain factors, like the beam span, the distance from adjacent beams, etc. In the example considered: beff,1=beff,2=0.50 m à beff=0.50+0.30+ 0.50=1.30 m . Second analysis : a plane frame is analysed, where the influence of slabs is accounted for using triangular finite elements. The finite element size is taken equal to 0.30 m across the slab surface and 0.15 m across the slab perimeter. Two different analyses are performed in the project <B_b4>. Their resulting displacements are presented in the two following pages, while the results and conclusions are presented in the third. In both analyses all the stiffness factors are taken equal to 1.0, rigid bodies and shear effect are taken into account. The analyses results are compared by means of the crossbar stiffness at the third level. The same procedure is required for both analyses to some point: In the menu, select ‘Parameters’ à ‘Horizontal Forces’ à ‘Seismic Forces’. In the dialog opened for instance at the third level, enter the value 100 in the corresponding field (the remaining values should be zero). Then check the box ‘Apply seismic forces’ and finally press the ‘Solve Building’ button to perform analysis. For the first analysis, press directly the ‘Analysis Results’ button and then press simultaneously (keeping ‘Ctrl’ pressed) ‘Structure’, ‘Space Frame Model’, ‘Wireframe Displ.’ and ‘Show values’. For the second analysis, to view the ‘Analysis Results’, first perform finite element analysis, by pressing the ‘pi-FES’ button. First analysis: frame type structure, modelled with members,
under a horizontal force H acting at the 3rd level 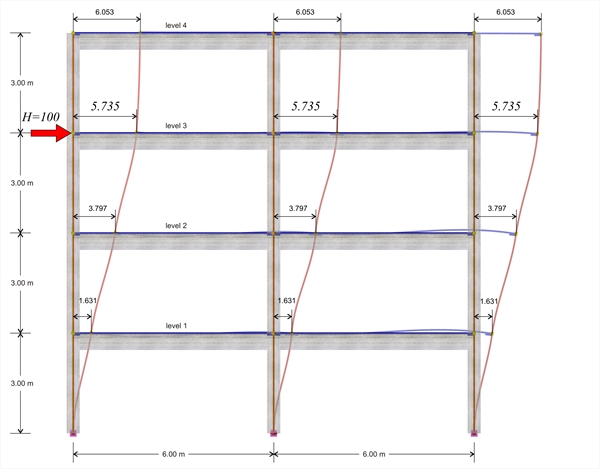 Figure B.4-2: The deformation of the structure
Figure B.4-2: The deformation of the structure Figure B.4-2: The deformation of the structure
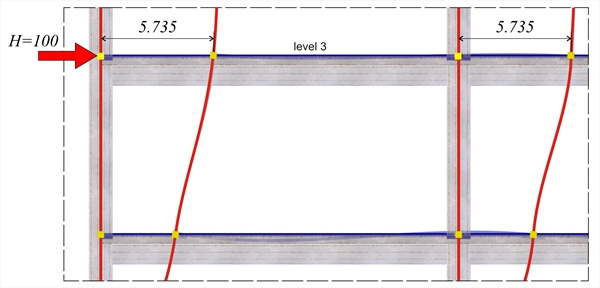 Figure B.4-3: Detail of deformation of members at the 3rd level (2nd storey)
Figure B.4-3: Detail of deformation of members at the 3rd level (2nd storey) Figure B.4-3: Detail of deformation of members at the 3rd level (2nd storey)
Second analysis: frame type structure, members and finite elements,
under a horizontal force H acting at the 3rd level 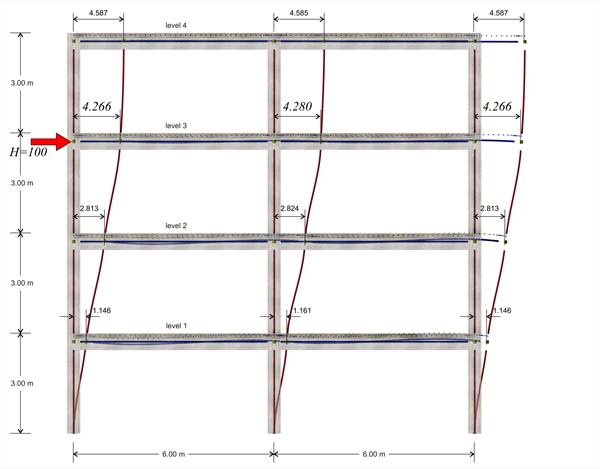 Figure B.4-4: The deformation of the structure
Figure B.4-4: The deformation of the structure Figure B.4-4: The deformation of the structure
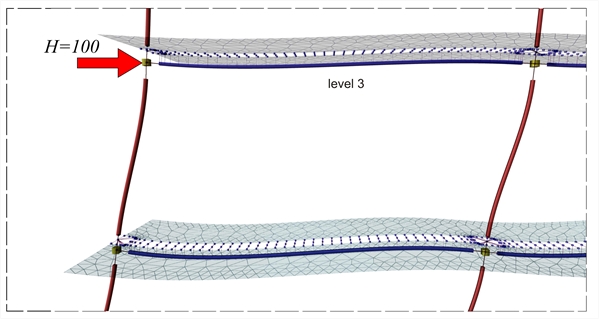 Figure B.4-5: Detail of members and finite elements deformation of the slab at the 3rd level (2nd floor)
Figure B.4-5: Detail of members and finite elements deformation of the slab at the 3rd level (2nd floor) Figure B.4-5: Detail of members and finite elements deformation of the slab at the 3rd level (2nd floor)
First analysis results: as shown in the previous pages, the displacement of the crossbar at the 3rd level, due the horizontal force H=100 kN, isδ3,1=5.735 mm, therefore its stiffness is K3,1=H/δ3,1 =100.0·103N/(5.735·10-3m)=17.4·106 N/m. The following elastic displacements δi,1 and stiffnesses Ki,1 are obtained from similar analyses applying force H=100 kN separately on each floor i. 4th level: H=100 kN, δ 4,1 =8.051 mm, K4,1=12.4·106 N/m 3rd level: H=100 kN, δ 3,1 = 5.735 mm , K3,1=17.4·106 N/m 2nd level: H=100 kN δ 2,1 =3.500 mm, K2,1=28.6·106 N/m 1st level: H=100 kN, δ 1,1 =1.358 mm, K1,1=73.6·106 N/m Second analysis results: as shown in the previous page, the displacement of the crossbar at the 3rd level, due to horizontal force H=100.0 kN, isδ3,2=4.266 mm, therefore its stiffness yields K3,2=H/δ3,2 =100.0·103N/(4.266·10-3m)=23.4·106 N/m. The following elastic displacements δi,1 and stiffnesses Ki,1 are obtained from similar analyses due to the force H=100 kN separately on each floor i. 4th level: H=100 kN, δ 4,2 =6.073 mm, K4,2=16.5·106 N/m 3rd level: H=100 kN, δ 3,2 = 4.266 mm , K3,2=23.4·106 N/m 2nd level: H=100 kN δ 2,2 =2.528 mm, K2,2=39.6·106 N/m 1st level: H=100 kN, δ 1,2 =0.886 mm, K1,2=112.9·106 N/m In the example considered, at the 3rd level, the stiffness obtained from the finite element analysis is higher by (23.4-17.4)/17.4= 34% and at the 4th, 2nd και 1st level, is higher by 33%, 38% 53% respectively. Conclusion : The frame stiffness derived from the finite element analysis is higher.
Β.5 Effect of walls on stiffnesses using finite elements As the effect of slabs on stiffness was examined in the previous paragraph, in order to obtain comparable results, a two-bay frame without slabs is considered next. Indicatively a four-storey frame with 3.0 m high columns is analysed. Each floor comprises two columns of 400/400 cross-section, one wall of 2000/300 cross-section and two beams of 6.0 m span and 300/500 cross-section. Columns and beams are modelled with members, while walls are modelled with members and rigid bodies at their tops, or with triangular finite elements. Two analyses are performed: First analysis : plane frame, whose walls are modelled with members and rigid bodies at their tops. Second analysis : plane frame, whose walls are modelled with triangular finite elements. The finite element size is taken equal to 0.30 m across the slab surfaced and 0.15 m across the slab perimeter. In both analyses, all the stiffness factors are taken equal to 1.0, while rigid bodies and shear effect are taken into account. The analyses results are compared by means of the crossbar stiffness of the third level. The displacements and stiffnesses derived from the analyses are presented in the following two pages. Project < B_b5>.
First analysis: Dual type structure, modelled with members,
under horizontal force H acting at the 3rd level,
 Figure B.5-1: The deformation of the structure
Figure B.5-1: The deformation of the structure Figure B.5-1: The deformation of the structure
First analysis results: The displacement of the crossbar at the 3rd level, due to horizontal force H=100 kN, is δ3,1=1.552 mm, therefore its stiffness is K3,1=H/δ3,1=100.0 ·103N/(1.552·10-3m)=64.4·106 N/m. The following elastic displacements δi,1 and stiffnesses Ki,1 are obtained from similar analyses applying force H=100 kN separately on each floor i. 4 η level: H=100 kN, δ 4,1 =3.033 mm, K4,1=33.0·106 N/m 3rd level: H=100 kN, δ 3,1 = 1.552 mm , K3,1=64.4·106 N/m 2 η level: H=100 kN δ 2,1 =0.629 mm, K2,1=159.0·106 N/m 1 η level: H=100 kN, δ 1,1 =0.146 mm, K1,1=685.0·106 N/m
Second analysis: Dual type structure, modelled with members and triangular finite elements, under horizontal force H acting at the 3rd level
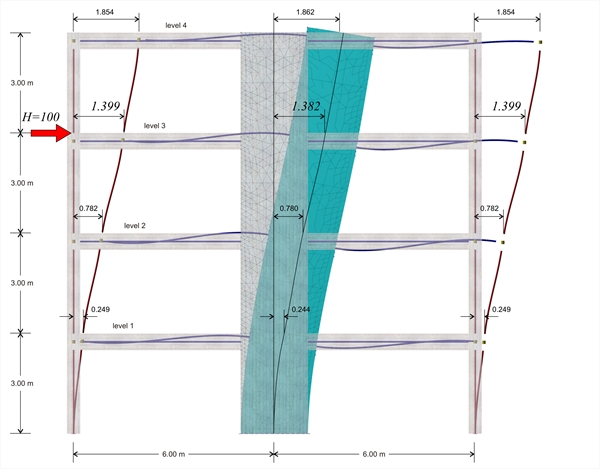 Figure B.5-2: The deformation of the structure
Figure B.5-2: The deformation of the structure Figure B.5-2: The deformation of the structure
Second analysis results: The displacement of the crossbar at the 3rd level, due to horizontal force H=100.0 kN, is δ3,2=1.399 mm, therefore its stiffness yields K3,1=H/δ3,1=100.0 ·103N/(1.399·10-3m)=71.5·106 N/m. The following elastic displacements δi,1 and stiffnesses Ki,1 are obtained from similar analyses applying force H=100 kN separately on each floor i. 4th level: H=100 kN, δ4,2=2.783 mm, K4,2=35.9·106 N/m 3rd level: H=100 kN, δ 3,2 = 1.399 mm , K3,2=71.5·106 N/m 2nd level: H=100 kN δ2,2=0.543 mm, K2,2=184.0·106 N/m 1st level: H=100 kN, δ1,2=0.117 mm, K1,2=855.0·106 N/m In the example considered, at the 3rd level, the stiffness obtained using finite element modelling is (71.5-64.4)/64.4=11% higher, while at the 4th, 2nd and 1st level 9%, 16% and 25% higher, respectively. Conclusion : The frame stiffness slightly differs when walls are modelled with two-dimensional finite elements. |