Multistorey plane dual systems|www.BuildingHow.com

VOLUME A
The art of construction and detailing
Introduction
The structural frame
- Introduction
- Structural frame elements
  - Columns
  - Beams
  - Slabs
  - Staircases
  - Foundation
- STRUCTURAL FRAME LOADING
- BEHAVIOR OF THE STRUCTURAL FRAME
  - The behavior and reinforcement of a slab
  - Behavior and reinforcement of beams and columns
Construction methods
- The materials
- The moulds
- Thermal insulation of structural elements
- Concrete
- The steel
- Reinforcement specifications of antiseismic design
- Industrial stirrups - stirrup cages
- Standardized cross-sections of reinforced concrete elements
Reinforcement
- Columns
- Shear walls
- Composite elements
- Beams
- Slabs
- Staircases
- Foundation
Quantity surveying
- Estimation of the concrete’s quantity
- Estimation of the formworks’ quantity
- Estimation of the spacers’ quantity
- Estimation of the reinforcements' quantity
- Total estimation of the materials’ quantities
- Optimization of the reinforcement schedule
- Estimation of the structural frame’s cost
- Electronic exchange of designs - bids - orders
Detailing drawings
- General
- The drawings’ title block
- Carpenter’s drawings
- Steel fixer’s drawings
Tables
- Table 1
- Table 2
- Table 3
Drawings
- Carpenter’s drawings
- Steel fixer’s drawings
Model (exemplary) construction

« Multistorey plane frame systems Comparison of multistorey frame and dual systems »

Multistorey plane dual systems

In the following multistorey plane frame of project <B_532> the interstorey fluctuation of the apparent stiffness factors k_j and the moment distribution factor a_j in both columns and wall is presented.

Figure 5.3.2-1: Four-storey dual type structure comprising two columns and a wall

If the frame also comprises walls, the differences in stiffnesses and in moment distributions become more intense as the number of stories increase.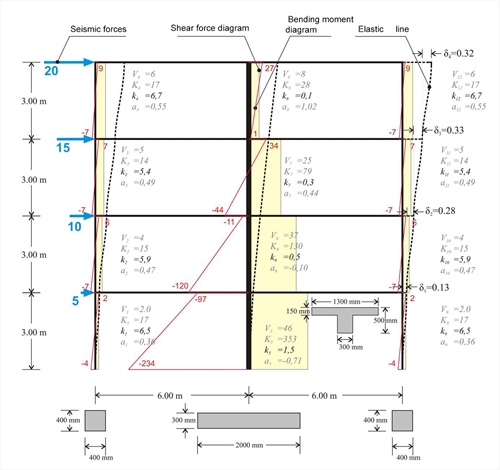

Figure 5.3.2-2: Multistorey dual type structure with triangular distribution of seismic forces( "hand-made" graphical representation)

Example 5.3.2 (3^rd storey) :

Column stiffnesses: K_3,1=4.6/0.329=14,K_3,2=25.9/0.329=79 K_3,3=4.6/0.329=14.

Storey stiffness: Κ ₃ = (20+15)/0.329=107. The apparent relative stiffness of the storey can also derive from the sum of its column stiffnesses, i.e. K₃= K_3,1+K_3,2+ K_3,3=107.

If shear effect is taken into account (Shear effect=ON), the displacements are δ ₁ =0.14, δ ₂ =0.30, δ ₃ =0.34, δ ₄ =0.32 mm, i.e. the difference is small.

If, however, rigid bodies effect is taken into account (Rigid body=ON), the displacements obtained are significantly smaller equal to δ ₁ =0.12, δ ₂ =0.22, δ ₃ =0.24, δ ₄ =0.21 mm, leading to much larger stiffness values.

In case of a basement, zero seismic forces are developed at its roof level. However the fixed end condition applies at the bases only of the columns located at the basement perimeter walls.

In the multistorey dual frame, the column factors are characterized by relatively small fluctuations with k varying from 5 to 7 and a from 0.35 to 0.55. On the contrary the corresponding fluctuation in the wall factors is significant with k varying from 0.10 to 1.50 and a from 1.0 to -1.0 [*] Note NoteIn case the frame has more storeys, the value of factor k decreases further. It should be noted that it could reach even negative values in the upper storeys. In such cases walls have an unfavourable effect on frames. Consequently, it is therefore pointed out, that although walls behave in a relieving way in the lower storeys, in the upper ones they might even behave in a negative way. To this end it is recommended to use dual systems in multistorey buildings. In dual systems, walls function effectively in the lower storeys, while frames in the upper ones. .

« Multistorey plane frame systems Comparison of multistorey frame and dual systems »