For the horizontal components of the seismic action the design spectrum, S_d(T), is defined by the following expressions:

0 ≤ T < T_B:

T_B ≤ T < T_C:

T_C ≤ T < T_D:

T_D ≤ T:

The recommended value, provided by the EC8, for β is 0.20.

Example : for importance class II → γ_I = 1.0, soil type B → S = 1.2, seismic zone witha_gR = 0.24 and q = 4.5, for values of Τ 0.1, 0.25, 1.0 and 3.0, the corresponding values of S_d are 0.171g, 0.16g, 0.08g and0.048g.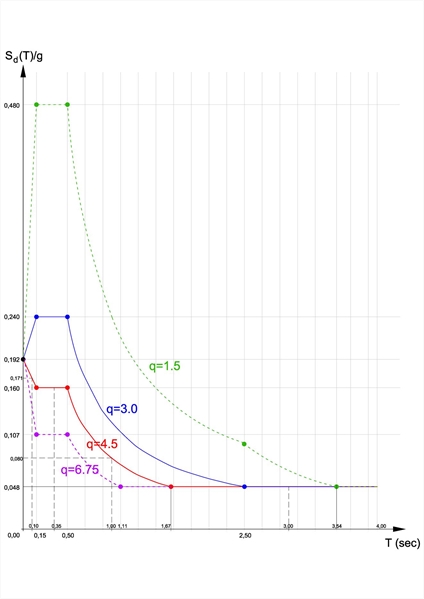

Figure 6.1.6: Design spectrum of horizontal actions (a) for q = 4.5, (b) for q = 3.0 and (c) for q = 1.5.Seismic zone with a_gR = 0.24, T_D = 2.5, soil type B, importance class ΙΙ

Figure 6.1.6: Design spectrum of horizontal actions (a) for q = 4.5, (b) for q = 3.0 and (c) for q = 1.5.Seismic zone with a_gR = 0.24, T_D = 2.5, soil type B, importance class ΙΙ

Setting a_gR = 0.24, S = 1.2, γ _I = 1.0 yields γ _I · a_gR · S = 1.0 ·0.24·1,2 = 0.288.

The expressions for four different values of q are the following:

For q = 6.75 yields 2.5/q = 2.5/6.75 = 0.3703

0 ≤ T < 0.15: S_d (0) = 0.288·2/3 = 0.192, Sd(0.15) = 0.288·2.5/6.75 = 0.107 → straightline segment between points (0.0, 0.192), (0.15, 0.0107) S_d(T) = 0.288·[2/3+T/0.15· (2.5/6.75-2/3)] = 0.192-0.569T

0.15 ≤ T < 0.50: curve S_d(T) = 0.107 → straight line segment in the whole range

0.50 ≤ T < 2.50: curve S_d(T) = max ( γ _I · a_gR · S · 2.5/q[T_C/T], β · γ _I · a_gR) = max(0.107 · 0.50/T, 0.048) curvature point at Τ = 1.11 → straight line segment after Τ = 1.11

2.50 ≤ T < 4.0: curve S_d(T) = max( max ( γ _I · a_gR · S · 2.5/q[T_CT_D/T²], β · γ _I · a_gR) = max(0.107 · 1.25/T², 0.048) curvature point at Τ = 1.67 → straight line segment in the whole range

For q = 4.5 yields 2.5/q = 2.5/4.5 = 25/45 = 0.555555556

0 ≤ T < 0.15: S_d (0) = 0.288 · 2/3 = 0.192, S_d(0.15) = 0.288 · 25/45 = 0.16 → straight line segment between points (0.0, 0.192), (0.15, 0.16) Sd(T) = 0.288· [2/3+T/0.15 · (2.5/4.5-2/3)] = 0.192-0.213T

0.15 ≤ T < 0.50: curve S_d(T) = 0.16 → straight line segment in the whole range at 0.16

0.50 ≤ T < 2.50: curve S_d(T) = max ( γ _I · a_gR · S · 2.5/q[T_C/T], β · γ _I · a_gR) = max(0.16 · 0.50/T, 0.048) curvature point at Τ = 1.67 → straight line segment after Τ = 1.67

2.50 ≤ T < 4.0: curve S_d(T) = max( max ( γ _I · a_gR · S · 2.5/q[T_CT_D/T²], β · γ _I · a_gR) = max(0.16 · 1.25/T², 0.048) curvature point at Τ = 2.04 → straight line segment in the whole range

For q = 3.0 yields 2.5/q = 2.5/3.0 = 25/30 = 0.83333333333333

0 ≤ T < 0.15: S_d (0) = 0.288 · 2/3 = 0.192, S_d(0.15) = 0.288 · 0.83333333 = 0.24 → straight line segment between points (0.0, 0.192), (0.15, 0.24) Sd(T) = 0.288·[2/3+T/0.15 ·(2.5/3.0-2/3)] = 0.192+0.32T

0.15 ≤ T < 0.50: curve S_d(T) = 0.24 → straight line segment in the whole range

0.50 ≤ T < 2.50: curve S_d(T) = max ( γ _I · a_gR · S · 2.5/q[T_C/T], β · γ _I · a_gR) = max(0.24 · 0.50/T, 0.048) curvature point at Τ = 2.5 → straight line segment does not exist

2.50 ≤ T < 4.0: curve S_d(T) = max( max ( γ _I · a_gR · S · 2.5/q[T_CT_D/T²], β · γ _I · a_gR) = max(0.24 · 1.25/T², 0.048)

curvature point at Τ = 2.5 → straight line segment in the whole range at 0.048

For q = 1.5 yields 2.5/q = 2.5/1.5 = 25/15 = 0.83333333333333

0 ≤ T < 0.15: S_d (0) = 0.288·2/3 = 0.192, S_d(0.15) = 0.288·1.66666666666667 = 0.48 → straightline segment between points (0.0, 0.192), (0.15, 0.48) Sd(T) = 0.288·[2/3+T/0.15· (2.5/1.5-2/3)] = 0.192+1.92T

0.15 ≤ T < 0.50: curve S_d(T) = 0.48 → straight line segment in the whole range

0.50 ≤ T < 2.50: curve S_d(T) = max ( γ _I · a_gR · S · 2.5/q[T_C/T], β · γ _I · a_gR) = max(0.48 · 0.50/T, 0.048) curvature point at Τ = 5.0, → straight line segment does not exist

2.50 ≤ T < 4.0: curve S_d(T) = max( max ( γ _I · a_gR · S · 2.5/q[T_CT_D/T²], β · γ _I · a_gR) = max(0.48 · 1.25/T², 0.048) curvature point at Τ = 3.54 → straight line segment between Τ = 3.54 and Τ = 4.0 at 0.048

Design spectrum of vertical seismic actions [EC8, §3.2.2.5(5)]

The design of buildings usually does not account for the vertical component of the seismic action (see §6.6.2), but when it does it shall satisfy the following conditions:

• The design spectrum of §6.1.6 shall be adopted, replacing a_g with a_vg = 0.9a_g [EC8, §3.2.3, table 3.4]

• Soil factor S shall be taken equal to 1.0

• Behaviour factor q shall be taken equal or less than 1.5

When demanding conditions occur, e.g. in multistorey planted columns, it is imposed for the vertical accelerations to be taken into account and maybe even a uniform value q = 1.5 should be considered for the whole structure, used for the calculation of the horizontal accelerations.

In a serious case, it is useful to also consider the structure without the diaphragmatic behaviour of floors, at least at nodes where particularities exist, so that an exact value of the vertical seismic acceleration is obtained at the critical nodes.

For practical and safety reasons, the vertical acceleration of critical nodes may be taken equal to the maximum vertical accelerationa_V occurred at any node. This maximum vertical acceleration is equal to a_V,max = 0.9·γ_I·a_gR·2.5/1.5 → a_V,max = 1.5·γ_I ·a_gR.