MODELLING SLABS WITH FINITE ELEMENTS A.1 Modelling slabs with finite elements in a structural frame In order to investigate the ways that: 1) the frame behaviour at the regions close to columns, 2) the deflection of beams and 3) the torsional stiffness of beams,α affect the behaviour of slabs, two equivalent models of the simple structure illustrated in the figure, are created using the related software: (i) one model using members and (ii) one model using finite elements  Figure A.1-1: The structure of project of the related software(columns cross-section 400/400, beams cross-section 300/500, slab thickness 170 mm)
Figure A.1-1: The structure of project of the related software(columns cross-section 400/400, beams cross-section 300/500, slab thickness 170 mm) Figure A.1-1: The structure of project of the related software(columns cross-section 400/400, beams cross-section 300/500, slab thickness 170 mm) ( i ) Model using members Consider the project <B_336> in the related software. Joists are arranged on a 1.00 m x 1.00 m grid, where the main joists have cross-sections 500/170 and the secondary joists have cross-sections 200/170. Dead and live loads on the main joists, based on which the total load of a strip withwidth 1.0 m will be calculated, is equal to 3.4 kN/m2 and 5.0 kN/m2 respectively. Also, to ignore rigid bodies, the parameter "Model Parameter" → " Rigid Body Type" should be set to 0, thus resulting in a simpler model.  Figure A.1-2: Slab modelled with members, which correspond to 2 beams b1 and b2 with cross-section 300/500,to 6 main joists (of the slab) b3 to b8 with cross-section 500/170 and3 secondary joists (of the slab) with cross-section 200/170(project , related software)
Figure A.1-2: Slab modelled with members, which correspond to 2 beams b1 and b2 with cross-section 300/500,to 6 main joists (of the slab) b3 to b8 with cross-section 500/170 and3 secondary joists (of the slab) with cross-section 200/170(project , related software) Figure A.1-2: Slab modelled with members, which correspond to 2 beams b1 and b2 with cross-section 300/500,to 6 main joists (of the slab) b3 to b8 with cross-section 500/170 and3 secondary joists (of the slab) with cross-section 200/170(project , related software)
( ii ) Model using finite elements In all the following examples the pi-FES software is used and the same basic project <B_331> unchanged. Certain parameters change in some cases. 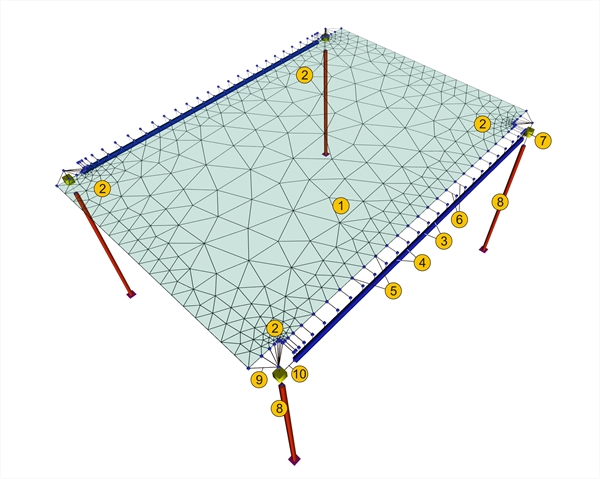 Figure A.1-3: Slab model with triangular finite elements (project , pi-FES of the related software)
Figure A.1-3: Slab model with triangular finite elements (project , pi-FES of the related software) Figure A.1-3: Slab model with triangular finite elements (project , pi-FES of the related software) 1. "triangular finite element" 2. "refinement region of finite elements" 5. "nodes of slab-beam connections" 6. "rigid bodies of slab supports" 7. "master node of column " 9. "rigid bodies of slab-column connection" 10. "rigid body of column-beam connection"
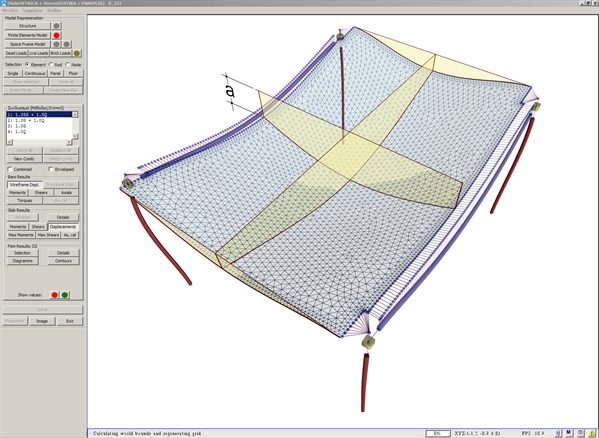 Figure A.1-4: Deformed structure and cross-sections of deformed slab (a=common beam-slab deflection)
Figure A.1-4: Deformed structure and cross-sections of deformed slab (a=common beam-slab deflection) Figure A.1-4: Deformed structure and cross-sections of deformed slab (a=common beam-slab deflection)
The finite element model in all the examples of this chapter is based on the following meshing parameter values: - Overall finite element size: 0.10 m
- Perimeter finite element size: 0.05 m
While the results are represented according to the following parameters: - Stress resultants diagrams per 1.0 m along X and along Y
- Transparent displaced structure
In all following examples, the slab stress resultants will be compared to the stress resultants of the typical simply supported member of the slab with width 1.0 m and length 4.0 m as stated in §3.2. In a simply supported strip of the slab the support moments are equal to 0.0 and the span moment w·l2/8=14.59 ·4.02/8=29.2 kNm. In the main joist fixed at both ends the support moments are equal to -w·l2/12=-14.59·4.02/12=-19.5 kNm and the respective span moment to w·l2/24=14.59 ·4.02/24=9.7 kNm.
A.1.1 The frame behaviour in the regions close to columns In order not to involve the issues of frame behaviour and beam torsional stiffness, the latter is considered insignificant. "Model Parameters" → "Torsional Inertia Factor=0.01". A.1.1.1 Model using members In the model using members (project <B_336>), the two main end joists (of the slab) together with the columns behave as a frame. As a result, high negative bending moments are developed,Μ=-26.4 kNm corresponding to ratio (-26.4)/(-19.5)=135% of the fixed-ended member and relatively weak positive bending moments, M=+15.6 kNm in their middle, corresponding to ratio 15.6/29.2=53% of the simply supported member. The end main joists, that form frames with columns, have greater stiffness than the middle almost simply supported joists and to this end, they carry higher load and result in high support moments. The middle main joists are supported on the ends through the secondary joists. Consequently, the secondary joists are stressed from not insignificant positive bending moments M=7.1 kNm corresponding to ratio 7.1/29.2=24% of the simply supported member. In the middle main joists, the span moments are high M=22.6 kNm to 29.1 kNm approximating the theoretical moments of the simply supported member in the middle area of the slab. 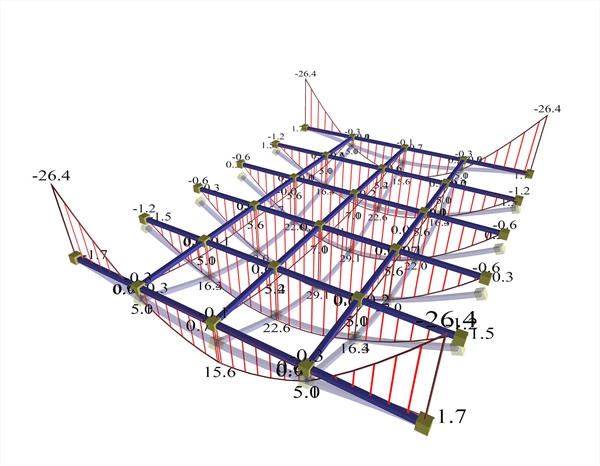 Figure A.1.1.1-1: The end main joists behave like a frame.Negative moments at the ends (regions of columns) should be carried by negative reinforcement.(project , pi-FES of related software)
Figure A.1.1.1-1: The end main joists behave like a frame.Negative moments at the ends (regions of columns) should be carried by negative reinforcement.(project , pi-FES of related software) Figure A.1.1.1-1: The end main joists behave like a frame.Negative moments at the ends (regions of columns) should be carried by negative reinforcement.(project , pi-FES of related software)
The slab model with continuous members is more accurate than the assumption of a slab simply supported along its whole length. However, in order for the actual structure to behave as designed in this case, the slab-column connection regions (edges of end main joists) should be reinforced, where (as already mentioned) high negative bending moments are developed. In case the dimensioning and the reinforcement calculation of the end main joists are done according to this analysis, but the slab-columns connection regions are not reinforced properly, then the reinforcements in these regions will yield, resulting in the supports of the end main joists to mutate into simply supported (i.e. the degree of fixity will be reduced to zero→ hinge). Consequently, on the span, almost twice the estimated moments will appear and the slab will not be able to resist with the existing reinforcement. 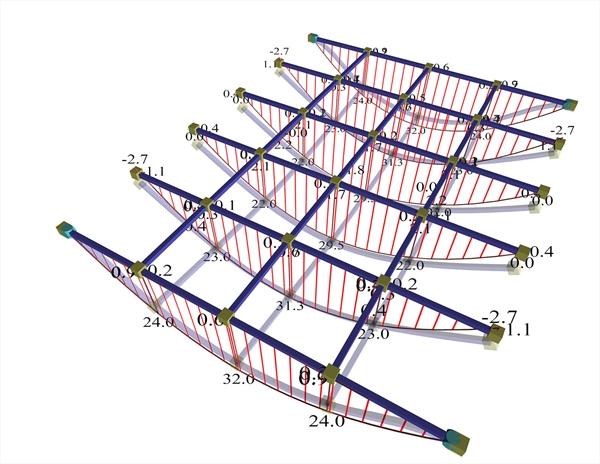 Figure A.1.1.1-2: The end main joists are considered simply supported.Moment diagrams of all main joists approach the simply supported condition.
Figure A.1.1.1-2: The end main joists are considered simply supported.Moment diagrams of all main joists approach the simply supported condition. Figure A.1.1.1-2: The end main joists are considered simply supported.Moment diagrams of all main joists approach the simply supported condition. In order to place pin supports on the two end joists press "beam" → "Parameters" →"hinge on the left and right". The support condition of the end main joists allow for a free vertical rotation (φy=0). In this case, the moments of all the main joists M=32.0 to 29.5 kNmpractically correspond to the moment of the simply supported member (M=29.2 kNm), while in the secondary direction moments are insignificant (M=2.1 kNmcorresponding to 2.1/29.2=7% of a simply supported moment).
Α.1.1.2 Model with finite elements The slab model using two-dimensional finite elements provides more accurate results (project <B_331>, pi-FES of the related software). The parameter values used in all the examples i.e. values for stiffnesses for beams, columns and slabs are equal to 1.0, i.e. stiffnesses of all elements are considered to be equal to the elastic ones and the torsional stiffness of beams is taken as being equal to 0.01 of the elastic one. 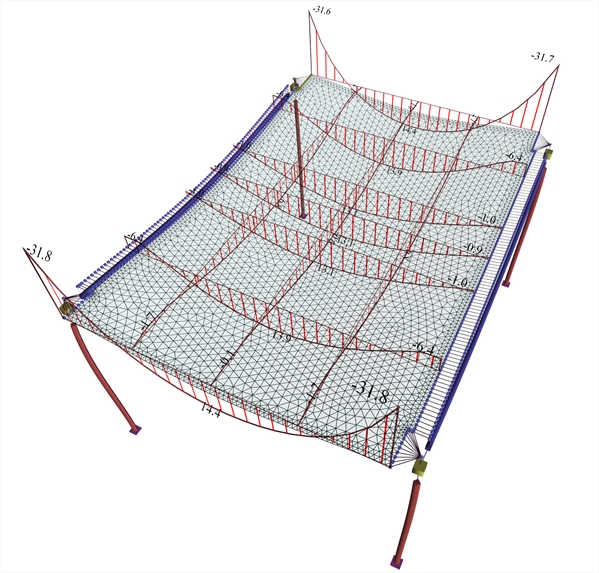 Figure A.1.1.2: The end main strips effectively function as frames.Negative moments at the ends (regions of columns) need to be carried by negative reinforcement.(project , pi-FES of the related software)
Figure A.1.1.2: The end main strips effectively function as frames.Negative moments at the ends (regions of columns) need to be carried by negative reinforcement.(project , pi-FES of the related software) Figure A.1.1.2: The end main strips effectively function as frames.Negative moments at the ends (regions of columns) need to be carried by negative reinforcement.(project , pi-FES of the related software) The results resemble those of the model using members with the following differences. In end main strips (corresponding to end main joists of §Α.1.1.1), the frame behaviour is more intense because support moments are higher, M=-31.8 kNm corresponding to ratio (-31.8)/(-19.5)=163% of the fixed-ended member and span moments are lower, M=+14.4 kNm corresponding to 14.4/29.2=49% of the simply supported member. In middle main zones (corresponding to middle main joists), span moments are lower, M=+13.9 and +13.1 kNm corresponding to13.9/29.2=48% of the simply supported member. Span moments of secondary zones (corresponding to secondary joists of the §Α.1.1.1) are higher, M=9.0 kNm corresponding to 9.0/29.2=31% of the simply supported member, due to the fact that the internal torsional stiffness of slab elements (twist) is stronger than the corresponding of members. The note of §Α.1.1.1 (members) is also applicable here, regarding the need for appropriate reinforcement of negative moment support regions at the end main strips, so that the calculated stresses apply in the actual structure as well. Positive moments (of small range) at the connection of the slab finite elements with the beam are developed due to the fact that the zero value of this bending moment diagram occurs in the position of the centroidal axis of the beam. Α.1.1.3 First Conclusion For construction in common worksites, slab analysis using finite elements should assume pinned supports on columns. Except from the minimum negative reinforcement at the slab supports, increased and mainly well anchored negative reinforcement is required at the column regions. In the absence of more accurate calculation of the negative reinforcement, grid reinforcement is recommended, equal to the slab span reinforcement, placed in distance equal to the column cross-sectional dimension increased at both sides by the minimum cross-sectional dimension of the column. The traditional structural analysis considers beams as practically undeformed. In general, this assumption, applies also to modern structural analysis. However, disposing of more accurate analysis methods (finite elements), one is under the impression that it is not any more necessary possible to form structures with beams of remarkably higher stiffness against slabs. The supporting beams, especially in earthquake resistant structures, have significantly higher moment of inertia compared to the slab strips. Depending on the spans and the support types, beam deflection is as a rule significantly smaller than the slab deflection. Each differential deflection of beams causes a redistribution of slab moments compared to the assumption of non-deformable supports of the slabs on the beams. The question raised concerns the order of magnitude of these differences.
Α.1.2.1 Model using members The project <B_336> is used in 3 variations for 1000, 500 and 300 mm height of supporting beams. Supporting beams 300/1000 : 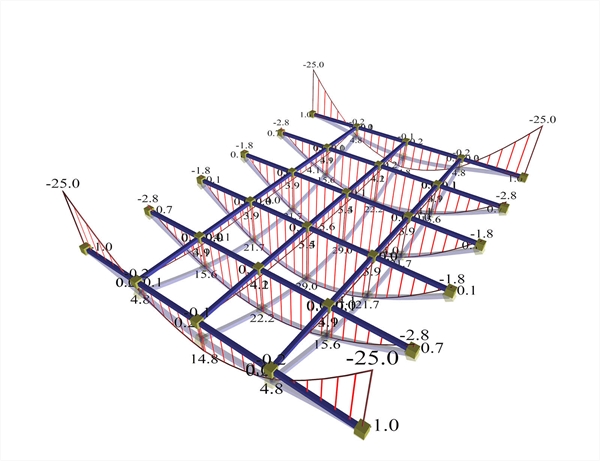 Figure A.1.2.1-1: Supporting beams, cross-section 300/1000.The effect of beam deflections on the deformation of the slab is insignificant.
Figure A.1.2.1-1: Supporting beams, cross-section 300/1000.The effect of beam deflections on the deformation of the slab is insignificant. Figure A.1.2.1-1: Supporting beams, cross-section 300/1000.The effect of beam deflections on the deformation of the slab is insignificant. Moments developed in the main direction are M=14.8, 22.2 and 29.0 kNm corresponding to ratio 14.8/29.2=51%, 22.2/29.2=76% and 29.0/29.2=99% of the simply supported member. The maximum moment developed in the secondary direction is M=5.5 kNm corresponding to ratio 5.5/29.2=19% of the simply supported member. Negative moments developed, are M=-25.0 kNm corresponding to ratio (-25.0)/(-19.5)=128% of the fixed-ended member. Beam deformations are practically insignificant with respect to those of the slab. Therefore, differential joist deformations in both directions give practically zero difference of moments in both directions.
Supporting beams 300/500 :
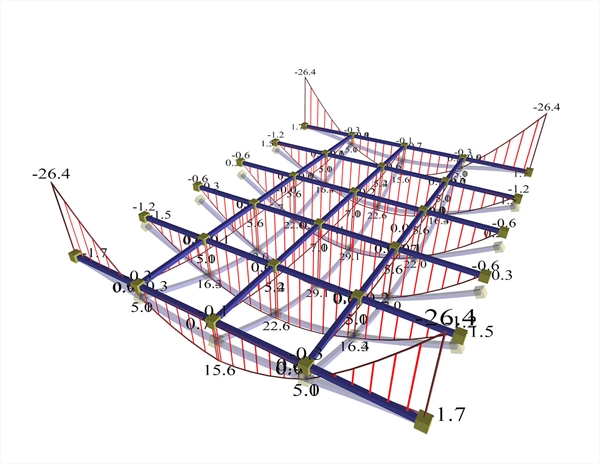 Figure A.1.2.1-2: Supporting beams, cross-section 300/500.The effect of differential deformation of slab and corresponding moments is moderate.
Figure A.1.2.1-2: Supporting beams, cross-section 300/500.The effect of differential deformation of slab and corresponding moments is moderate. Figure A.1.2.1-2: Supporting beams, cross-section 300/500.The effect of differential deformation of slab and corresponding moments is moderate. Moments developed in the main direction are M=15.6, 22.6 and 29.1 kNm corresponding to a ratio 15.6/29.2=53%, 22.6/29.2=77% and 29.1/29.2=100% of the simply supported member. The maximum moment developed in the secondary direction is M=7.0 kNm corresponding to a ratio 7.0/29.2=24% of the simply supported member. Negative moments developed, are M=-26.4 kNm corresponding to a ratio (-26.4)/(-19.5)=135% of the fixed-ended member. Beam deformations continue to be significantly less than slab joists. The differential joist deformations in both directions cause quite small differences of moments in both directions.
Supporting beams 300/300 : Beam deformations are significant and visibly affect the deformations of the joists. High differential joist deformations in both directions give difference of moments in main direction of (34.9-27.3)/34.9=22% and in the secondary direction, secondary moments of 5.4/27.3=20% of the corresponding moment of the main direction. 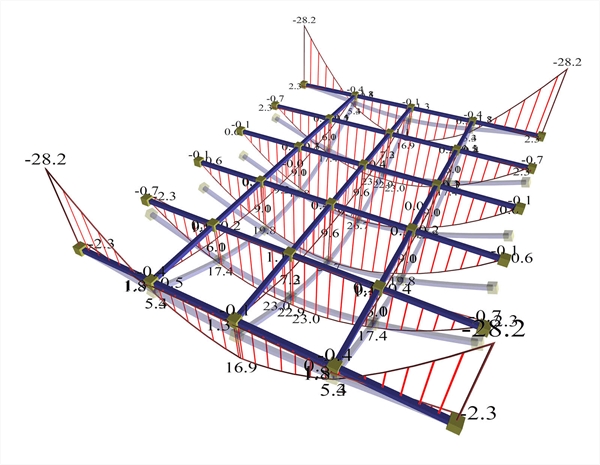 Figure A.1.2.1-3: Supporting beams, cross-section 300/300The effect of beam deflections on the deformation of slab is significant
Figure A.1.2.1-3: Supporting beams, cross-section 300/300The effect of beam deflections on the deformation of slab is significant Figure A.1.2.1-3: Supporting beams, cross-section 300/300The effect of beam deflections on the deformation of slab is significant Moments developed in the main direction are M=16.9, 23.0 and 26.7 kNm corresponding to a ratio 16.9/29.2=58%, 23.0/29.2=79% and 26.7/29.2=91% of the simply supported member. The maximum moment developed in the secondary direction is M=9.6 kNm corresponding to a ratio 9.6/29.2=33% of the simply supported member. Negative moments developed, are M=-28.2 kNm corresponding to a ratio (-28.2)/(-19.5)=145% of the fixed-ended member. Beam deformations are significant and they apparently affect the joists. High differential joist deformations in both directions give significant difference of moments in both directions. Note : Seismic forces induce additional deflections on beams, affecting in turn the slabs stresses. However, this fact is not taken into consideration, because at the time of earthquake reduced loads are assumed G+ ψ2 · Q in the slabs where ψ2 =0.30 for humans loads, while the ultimate limit state for slabs takes into account (almost double) loads γG · G+ γQ · Q , where the normal values of the safety factors are equal to γG =1.35 and γQ =1.50 .
Α.1.2.2 Model using finite elements The project <B_331> is used in the same three variations as using the member model, i.e. with 1000, 500 and 300 mm height of supporting beams Supporting beams 300/1000 : 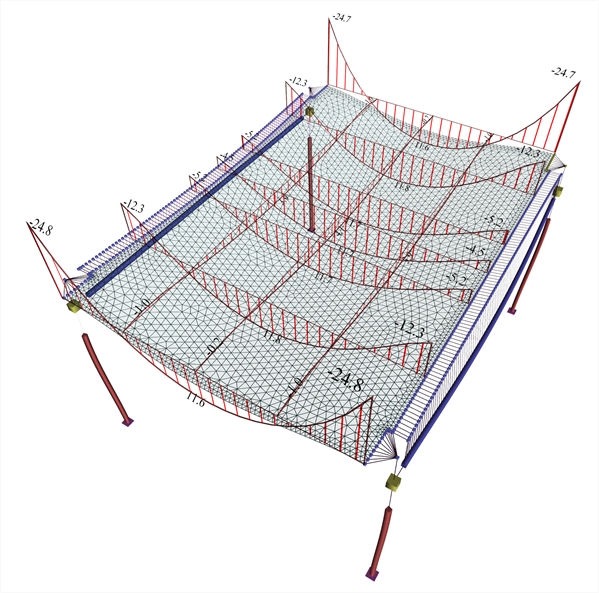 Figure A.1.2.2-1: Supporting beams, cross-section 300/1000.The effect of differential deformation of slab and corresponding moments is insignificant.
Figure A.1.2.2-1: Supporting beams, cross-section 300/1000.The effect of differential deformation of slab and corresponding moments is insignificant. Figure A.1.2.2-1: Supporting beams, cross-section 300/1000.The effect of differential deformation of slab and corresponding moments is insignificant. Moments developed in the main direction are M=11.6, 11.8 and 11.7 kNm corresponding to a ratio 11.6/29.2=40%, 11.8/29.2=40% and 11.7/29.2=40% of the simply supported member. The maximum moment developed in the secondary direction is M=4.1 kNm corresponding to a ratio 4.1/29.2=14% of the simply supported member. Negative moments developed, are M=-24.8 kNm corresponding to a ratio (-24.8)/(-19.5)=127% of the fixed-ended member. Beam deformations are practically insignificant with respect to the deformations of slab. Differential deformations of slab strips in both directions give practically zero difference of moments in the main direction and almost zero additional difference in the secondary direction.
Supporting beams 300/500 :  Figure A.1.2.2-2: Supporting beams, cross-section 300/500.The effect of differential deformation of slab and corresponding moments is obvious.
Figure A.1.2.2-2: Supporting beams, cross-section 300/500.The effect of differential deformation of slab and corresponding moments is obvious. Figure A.1.2.2-2: Supporting beams, cross-section 300/500.The effect of differential deformation of slab and corresponding moments is obvious. Moments developed in the main direction are M=14.4, 13.9 και 13.1 kNm corresponding to a ratio 14.4/29.2=49%, 13.9/29.2=48% and 13.1/29.2=45% of the simply supported member. The maximum moment developed in the secondary direction is M=9.0 kNm corresponding to a ratio 9.0/29.2=31% of the simply supported member. Negative moments developed, are M=-31.8 kNm corresponding to a ratio (-31.8)/(-19.5)=163% of the fixed-ended member. Beam deformations are significantly lesser than deformations of slab strips. Differential displacements of slab strips in both directions give small additional difference of moments in the main direction and significantly additional difference in the secondary direction.
Supporting beams 300/300 : 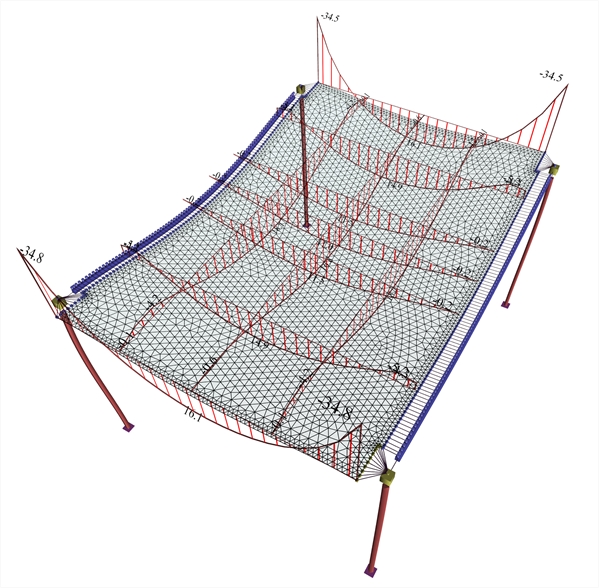 Figure A.1.2.2-3: Supporting beams, cross-section 300/300.The effect of differential deformation of slab and corresponding moments is obvious.
Figure A.1.2.2-3: Supporting beams, cross-section 300/300.The effect of differential deformation of slab and corresponding moments is obvious. Figure A.1.2.2-3: Supporting beams, cross-section 300/300.The effect of differential deformation of slab and corresponding moments is obvious. Moments developed in main direction are M=16.1, 14.9 και 11.5 kNm corresponding to a ratio 16.1/29.2=55%, 14.9/29.2=51% and 11.5/29.2=39% of the simply supported member. The maximum moment developed in the secondary direction is M=16.8 kNm corresponding to a ratio 16.8/29.2=58% of the simply supported member. Negative moments developed, are M=-34.8 kNm corresponding to a ratio (-34.8)/(-19.5)=178% of the fixed-ended member. Beam deformations are significant and they visibly affect the deformations of the slab strips. High differential displacements of strips along both directions give a relatively small difference of moments in the main direction but higher additional difference of moments in the secondary direction. Therefore, it should be noted that in the model with two-dimensional finite elements, the secondary bending moments are always significant, while the moments in the main direction remain relatively constant.
Α.1.2.3 Second Conclusion In conclusion, the assumptions of modelling frame elements using members and modelling slabs using two-dimensional finite elements to simulate are considered to be both logical and successful Moreover, the modelling is more successful the stronger the beams cross-section (mainly their depth) is, the smaller their span, and also the smaller the thickness of the slabs. The regulation imposes minimum ratio of slab reinforcement in the secondary direction equal to 20% of that corresponding to the main reinforcement, to carry the secondary, computable or not, stresses. In case where the beam height is roughly equal to the slab thickness (case of hidden beams), the use of beam members and independent slabs is worth only as a coarse model, providing a minimum static and dynamic model. In case the engineer adopts this assumption, secondary reinforcements should be placed in a higher ratio than the minimum one defined prescribed by the regulations. Α.1.3 Torsional stiffness of beams The general consideration of the effect of torsional stiffness as discussed in the §3.3.4, will be applied in the project <B_331> using finite elements and in project <B_336> using members. Cross-section of beams is 300/500. Three cases for the effect of torsional stiffness of beams will be examined: (a) fully elastic
(b) 10% of fully elastic
(c) 1% of fully elastic The user of the related software can modify the torsional stiffness of beams, by giving the desired value (1.00, 0.10, 0.01 corresponding to 100%, 10% and 1% of the elastic torsional stiffness respectively) in the 'Tortional Inertia Factor' parameter of 'Stiffness Parameters' dialog, located in menu 'Parameters'.
Α.1.3.1 Model using members (a) Torsional stiffness of beams: fully elastic 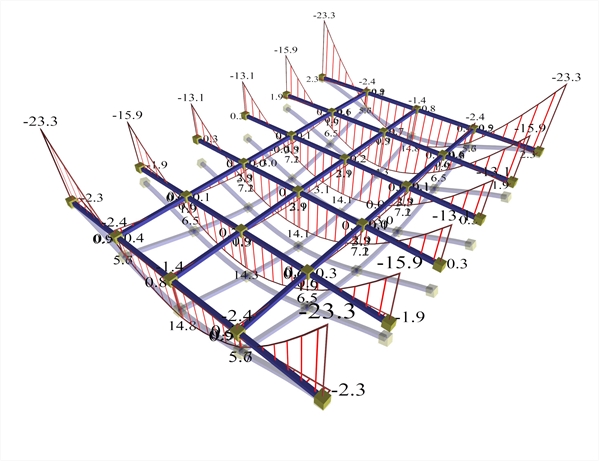 Figure A.1.3.1-1: Displacements and bending moments of the structure joists
Figure A.1.3.1-1: Displacements and bending moments of the structure joists Figure A.1.3.1-1: Displacements and bending moments of the structure joists
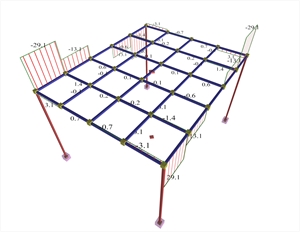 Figure A.1.3.1-2: Torsional moments of the structure beams
Figure A.1.3.1-2: Torsional moments of the structure beams Figure A.1.3.1-2: Torsional moments of the structure beams
Positive moments in the main direction areM=14.8, 14.3 and 14.1 kNm corresponding to a ratio 14.8/29.2=51%, 14.3/29.2=49% and 14.1/29.2=48% of the simply supported member. Negative moments in the main direction areM=-23.3, -15.9 and -13.1 kNm corresponding to a ratio (-23.3)/(-19.5)=119%, (-15.9)/(-19.5)=82% and (-13.1)/(-19.5)=67% of the fixed-ended member. Bending moments of the middle joists approach more the behaviour of the fixed-ended member rather than of the simply supported member. The two beams are stressed by high torsion, due to the support moments of joists (joists are supported on beams).
(b) Torsional stiffness of beams: 10% of fully elastic 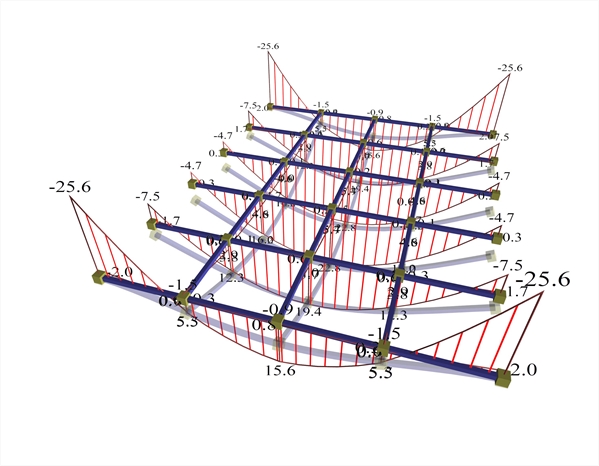 Figure A.1.3.1-3: Displacements and bending moments of the structure joists
Figure A.1.3.1-3: Displacements and bending moments of the structure joists Figure A.1.3.1-3: Displacements and bending moments of the structure joists
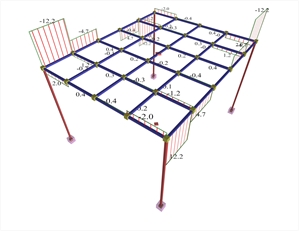 Figure A.1.3.1-4: Beam torsional moments
Figure A.1.3.1-4: Beam torsional moments Figure A.1.3.1-4: Beam torsional moments Positive moments developed in the main direction are M=15.6, 19.4 and 22.8 kNm corresponding to a ratio 15.6/29.2=53%, 19.4/29.2=66% and 22.8/29.2=78% of the simply supported member. Negative moments developed in the main direction are M=-25.6, -7.5 and -4.7 kNm corresponding to a ratio (-25.6)/(-19.5)=131%, (-7.5)/(-19.5)=38% and (-4.7)/(-19.5)=24% of the fixed-ended member. Bending moments of the middle joists approach more the behaviour of the simply supportedmember. The two beams are stressed by moderate torsion, due to support moments of joists (joists are supported on beams). (c) Torsional stiffness of beams: 1% of fully elastic  Figure A.1.3.1-5: Displacements and bending moments of the structure joists
Figure A.1.3.1-5: Displacements and bending moments of the structure joists Figure A.1.3.1-5: Displacements and bending moments of the structure joists
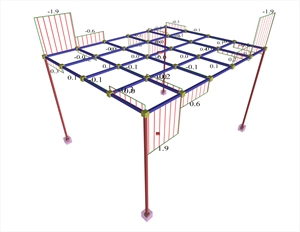 Figure A.1.3.1-6: Beams torsional moments
Figure A.1.3.1-6: Beams torsional moments Figure A.1.3.1-6: Beams torsional moments Positive moments developed in the main direction are M=15.6, 22.6 and 29.1 kNmcorresponding to a ratio 15.6/29.2=53%, 22.6/29.2=77% and 29.1/29.2=100% of the simply supported member. Negative moments developed in the main direction, in practice, are developed only at the end joists equal to M=-26.4 kNm corresponding to a ratio (-26.4)/(-19.5) =135% of the fixed-ended member. Bending moments of the middle joists correspond to the behaviour of the simply supported member. The two beams are not stressed by torsion, since the support moments of the main joists on beams are insignificant. Α.1.3.2 Model using finite elements (a) Torsional stiffness of beams: fully elastic 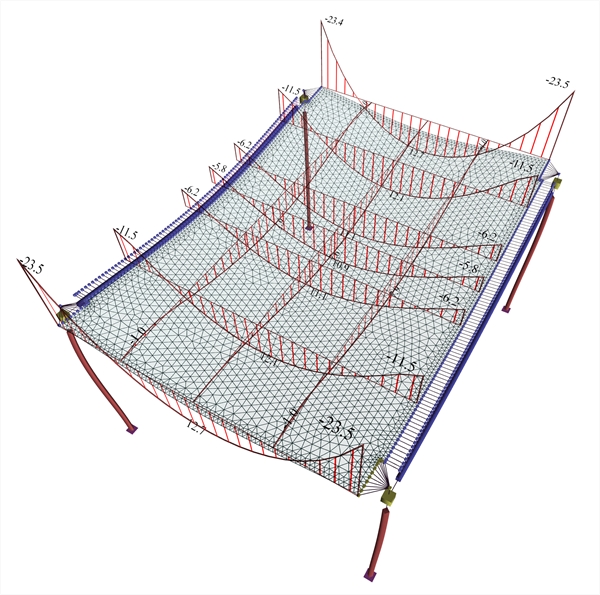 Figure A.1.3.2-1: Displacements and bending moments of the slab
Figure A.1.3.2-1: Displacements and bending moments of the slab Figure A.1.3.2-1: Displacements and bending moments of the slab
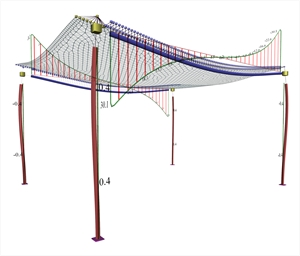 Figure A.1.3.2-2: Beams torsional moments
Figure A.1.3.2-2: Beams torsional moments Figure A.1.3.2-2: Beams torsional moments Positive moments developed in the main direction are M=12.7, 12.1 and 11.1 kNm corresponding to a ratio 12.7/29.2=43%, 12.1/29.2=41% and 11.1/29.2=38% of the simply supported member. Negative moments developed inthe main direction are M=-23.5, -11.5, και -6.2 kNm corresponding to a ratio (-23.5)/(-19.5)=121%,
(-11.5)/(-19.5)=59% are (-6.2)/
(-19.5)=32% of the fixed-ended member. Bending moments of strips approach the behaviour of the fixed-ended member. The two beams are stressed by high torsion. (b) Torsional stiffness of beams: 10% of fully elastic 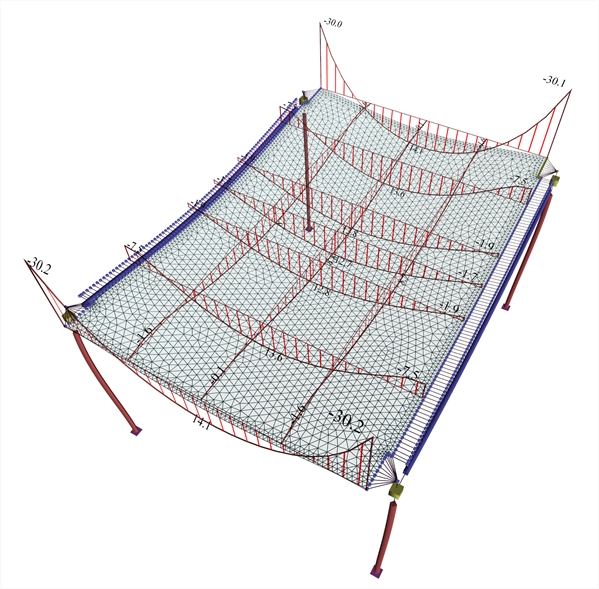 Figure A.1.3.2-3: Displacements and bending moments of the slab
Figure A.1.3.2-3: Displacements and bending moments of the slab Figure A.1.3.2-3: Displacements and bending moments of the slab
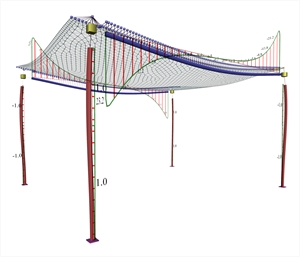 Figure A.1.3.2-4: Beams torsional moments
Figure A.1.3.2-4: Beams torsional moments Figure A.1.3.2-4: Beams torsional moments Positive moments developed in the main direction are M=14.1, 13.6 and 12.8 kNm corresponding to a ratio 14.1/29.2=48%, 13.6/29.2=47% and 12.8/29.2=44% of the simply supported member. Negative moments developed in the main direction are M=-30.2 and -7.5 corresponding to a ratio (-30.2)/(-19.5)=155%, and (-7.5)/(-19.5)=38% of the fixed-ended member. Bending moments of strips reflect an intermediate condition between the simply supported memberand the fixed-ended member. The two beams are stressed by moderate torsion.
(c) Torsional stiffness of beams: 1% of fully elastic  Figure A.1.3.2-5: Displacements and torsional moments of the slab
Figure A.1.3.2-5: Displacements and torsional moments of the slab Figure A.1.3.2-5: Displacements and torsional moments of the slab
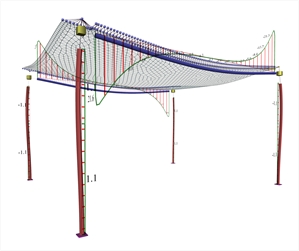 Figure A.1.3.2-6: Beams bending moments
Figure A.1.3.2-6: Beams bending moments Figure A.1.3.2-6: Beams bending moments Positive moments developed in the main direction are M=14.4, 13.9and 13.1 kNm corresponding to a ratio 14.4/29.2=49%, 13.9/29.2=48% and 13.1/29.2=45% of the simply supported member. Negative moments developed in the main direction are M=-31.8 and-6.4 kNm corresponding to a ratio
(-31.8)/(-19.5)=163%, and (-6.4)/
(-19.5)=33% of the fixed-endedmember. Bending moments of strips reflect an intermediate condition between the simply supported member andthe fixed-ended member. The two beams are stressed by lesser but not zero torsion.
Α.1.3.3 Third Conclusion Once the structure's formwork is removed, significant moments develop at the slab-beam connections, which are relieving slab bending and aggravating beam torsion. However, due to the creep of concrete, the torsional deformation of the beam increases gradually causing the reduction of torsional moments on the beam. The slab's bending moments are also accordingly reduced. Gradually this slab-beam deformation tends to develop the support intopinned. To this end EC2 in §6.3.1(2) states that '… in these cases it will normally be unnecessary to consider torsion at the ultimate limit state'. If torsional stiffness of beams and thus the relaxation of stress of the slab, are taken into account, beams should be necessarily dimensioned under torsion. Top reinforcement should be placed at the slab, properly shaped and anchored, and of course the beam should be reinforced the according to the detailing rules regarding torsion. Α.1.3.4 FINAL CONCLUSION , allowing the design of structures subject to bending. A slab strip can also be considered as an appropriate member. In the centroidal axis of this strip, moments and shear forces are being determined by integrating the appropriate stresses along the respective finite elements. The assumption of a structure withbeams of adequate depth, providing significant stiffness to the structural frames [4] [*] Note On the other hand, the need of Capacity Design under bending, i.e. the need of higher strength of columns than beams, leads to beams with shorter heights. To this end, the art of the engineer consists in selecting the best possible cross-sections. , results in a plain space frame model consisting of members, which is reliable for both analysis and design. Note On the other hand, the need of Capacity Design under bending, i.e. the need of higher strength of columns than beams, leads to beams with shorter heights. To this end, the art of the engineer consists in selecting the best possible cross-sections. , results in a plain space frame model consisting of members, which is reliable for both analysis and design. In conclusion, the assumption of the members for modelling structural frames and the consideration of independent functionality of slabs are both acceptable and, under certain circumstances, form an adequately reliable solution. In finite element analysis, the common assumption adopted for slab supports is practically: slabs supported on beams with (almost) zero torsional stiffness. Regardless of the calculation method, the minimum detailing provisions of the regulations regarding the minimum reinforcement (the secondary as well as the negative one) of slabs should be followed with diligence. |