Centre of mass and radius of gyration|www.BuildingHow.com

VOLUME A
The art of construction and detailing
Introduction
The structural frame
- Introduction
- Structural frame elements
  - Columns
  - Beams
  - Slabs
  - Staircases
  - Foundation
- STRUCTURAL FRAME LOADING
- BEHAVIOR OF THE STRUCTURAL FRAME
  - The behavior and reinforcement of a slab
  - Behavior and reinforcement of beams and columns
Construction methods
- The materials
- The moulds
- Thermal insulation of structural elements
- Concrete
- The steel
- Reinforcement specifications of antiseismic design
- Industrial stirrups - stirrup cages
- Standardized cross-sections of reinforced concrete elements
Reinforcement
- Columns
- Shear walls
- Composite elements
- Beams
- Slabs
- Staircases
- Foundation
Quantity surveying
- Estimation of the concrete’s quantity
- Estimation of the formworks’ quantity
- Estimation of the spacers’ quantity
- Estimation of the reinforcements' quantity
- Total estimation of the materials’ quantities
- Optimization of the reinforcement schedule
- Estimation of the structural frame’s cost
- Electronic exchange of designs - bids - orders
Detailing drawings
- General
- The drawings’ title block
- Carpenter’s drawings
- Steel fixer’s drawings
Tables
- Table 1
- Table 2
- Table 3
Drawings
- Carpenter’s drawings
- Steel fixer’s drawings
Model (exemplary) construction

« Diaphragmatic behaviour Centre of stiffness and elastic displacements of the diaphragm »

Centre of mass and radius of gyration

The inertial behaviour of a diaphragm having a mass Σ(m_i) is idealised by a ring of equivalent inertial massdistribution. The ring has a total mass Σ(m_i), its centre is theCentre of Mass C_M and its radius theRad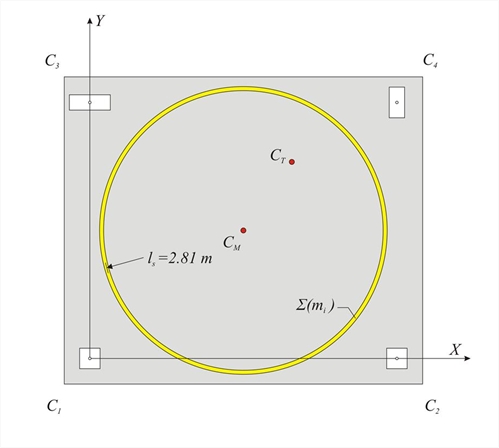ius of Gyration l_s.

Figure 5.4.2: The centre of mass C_M and the equivalent mass inertial ring with radius of gyration l_s

The coordinates of the centre of mass C_M of a diaphragm consisting of many mass points, linearly distributed, and surface masses linearly distributed derive from the expressions:

The radius of gyration l_s of the diaphragm with respect to the centre of mass C_M derives from the expression:

where Χ_i and Υ_i are the coordinates of each mass point m_i of the diaphragm, whereas I_pi is the polar moment of inertia of each mass m_i with respect to the centre of mass C_M.

According to the strength of materials, the polar moment of inertia of a mass m, whose centre is located at distance L from the centre of mass C_M of the diaphragm, depends on the distribution of the mass:

For a point mass: I_p=m·L²
For a mass linearly distributed along a segment of length l: I_p=m· (l²/12 + L²)
For a surface distributed mass in a rectangular shape of dimensions b,l: I_p=m· [(b²+l²)/12 + L²]
For a surface distributed mass in a triangular shape or a circular segment: the equivalent principal moment of inertia in respect to the centre of mass of this segment is calculated and the Steiner term m·L² is added.

Note:

In large floor plans, the radius of inertia can be calculated only from the reaction forces of the beams on the floor columns, while in case that the particular linear loads (e.g. of the walls) are distributed uniformly throughout the floor, the radius of inertia is calculated using the formula

where L_x, L_y are the dimensions of the floor plan.

Example 5.4.2

Centre of mass :

Due to symmetrical mass distribution, [*] Note NoteColumn self-weight is accounted for assuming that one-third of the load is applied to the top diaphragm and the remaining two-thirds to the base. The loads (and the corresponding masses) on the column tops are G1=4.0 kN, G2=4.0 kN, G3=6.0 kN and G4=4.5 kN, consequently there is a minimal deviation from the CM, i.e. with no practical difference from the geometrical centroid. Minimal differences also result, in case the small variations of the loads (masses) along the brick walls due to variation of column dimensions, as well as the extension of the slabs (designed in this way for supervisory purposes) are taken into account. X_CM=3.0 m and Y_CM=2.5 m.

Radius of gyration : [g=10 m/sec², therefore force F=1 kN corresponds to mass m=0.1 t.]

Slab: m₁=6.0m ·5.0m·0.71t/m²=21.3 t

b₁=6.0 m, l₁=5.0 m, L₁=0.0 m → I_p1=21.3t ·(6.0²+5.0²)m²/12=108.3 t·m²

Beam connecting C₁-C₂: m₂=6m·1.0t/m=6.0 t, l₂=6.0 m, L₂=2.5 m → I_p2=6.0· (6²/12+2.5²)=55.5 t·m²

Beam connecting C₃-C₄: likewise m₃=6.0 t, I_p2=55.5 t·m²

Beam connecting C₁-C₃: m₄=5.0m·1.0t/m=5.0 t, l₄=5.0 m, L₄=3.0 m → I_p4=5.0· (5.0²/12+3.0²)=55.4 t·m²

Beam connecting C₂-C₄ likewise m₅=5.0 t, I_p5=55.4 t · m²

Columns: m₆=0.1 ·(4.00+4.00+6.0+4.5)=1.85 t, L₆=√ (3.0²+2.5²)=3.905 m → I_p6=1.85 ·3.905²=28.2 t·m².

Finally Σ (m_i)=45.3 t and Σ (I_pi)=358.3 t · m²(2) → l_s=√[( Σ (I_p _ι )/ Σ (m_i)]=√(358.3/45.3)=2.81 m [*] Note Note If the same loads are uniformly distributed in plan, then ls=√[(Lx²+Ly²)/12]=√[(6.0²+5.0²)/12]=2.25 m

« Diaphragmatic behaviour Centre of stiffness and elastic displacements of the diaphragm »