|
« Space frames
Centre of mass and radius of gyration »
|
Floor slabs act in storey frames as strong horizontal elements, called diaphragms. Diaphragms are practically rigid and non-deformable and thus impose specific movements to the beams and the column tops.  Figure 5.4.1-1: Simple one-storey structure comprising four columns whose tops are connected by rigid slab-diaphragm.
Figure 5.4.1-1: Simple one-storey structure comprising four columns whose tops are connected by rigid slab-diaphragm. Figure 5.4.1-1: Simple one-storey structure comprising four columns whose tops are connected by rigid slab-diaphragm. 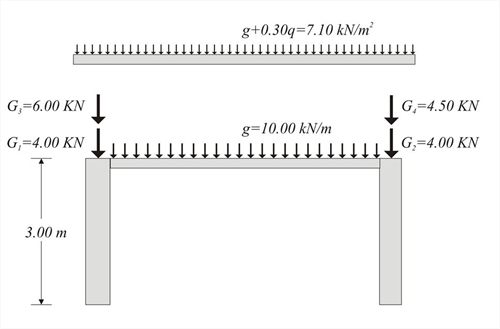 Figure 5.4.1-2: Loading Model
Figure 5.4.1-2: Loading Model Figure 5.4.1-2: Loading Model In case of an earthquake event, during which the main stresses are induced by the horizontal seismic actions, diaphragm action affects directly the behaviour of the whole structure. The diaphragmatic behaviour of structures of any type and size is presented in the following paragraphs. The simple four-column structure of the previous page is used as an example.
|
« Space frames
Centre of mass and radius of gyration »
|

|