Consider the typical floor of a multistorey building, with the centre of mass located in position X=9.0, Y=9.0 and the seismic force applied at theground floor is equal to 2000 kN. Calculate the displacements and stress resultants of columns C1, C3, C4, C 6, C11, C13, C16 under seismic action in direction X. The ground floor height is 3.0 m. Concrete class C30/37. 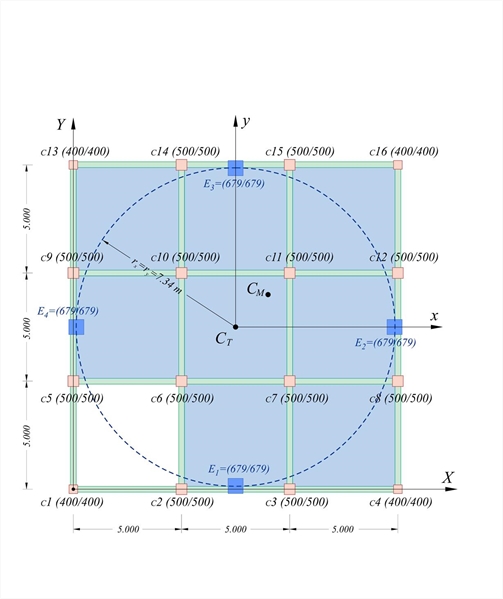 Figure 5.4.7.1
Figure 5.4.7.1 Figure 5.4.7.1 Select sheet B_547-1 of file "diaphragm_ortho.xls" containing the geometry of the 16 columns, the coordinates of centre of mass CM 9,00/9,00 and the seismic force Hx=2000 kΝ . Column C1 -although non diaphragmatic will be treated as belonging to the diaphragm as two beams frame into it and therefore behaves rather as a diaphragm one than as an inactive element.
| δ x | δ y | Vx | Vy | Mx,1 | Mx,2 | My,1 | My,2 | | | (mm) | (mm) | (kN) | (kN) | (kNm) | | | | | C1 | 3,67 | 0,97 | 47,5 | 12,6 | 71,3 | -71,3 | 18,8 | -18,8 | | C3 | 3,67 | -0,32 | 116,0 | -10,2 | 174,0 | -174,0 | -15,3 | 15,3 | | C4 | 3,67 | -0,97 | 47,5 | -12,6 | 71,3 | -71,3 | -18,8 | 18,8 | | C6 | 4,31 | 0,32 | 136,4 | 10,2 | 204,6 | -204,6 | 15,3 | -15,3 | | C11 | 4,96 | -0,32 | 156,9 | -10,2 | 235,3 | -235,3 | -15,3 | 15,3 | | C13 | 5,60 | 0,97 | 72,6 | 12,6 | 108,9 | -108,9 | 18,8 | -18,8 | | C16 | 5,60 | -0,97 | 72,6 | -12,6 | 108,9 | -108,9 | -18,8 | 18,8 | The coordinates of the centre of stiffness CT are at point 7.50, 7.50 as expected due to the symmetric geometry of the columns. rx=7.34 m, ry=7,34 m, θz= -0,00012914, Kθ=23.230,8 MNm, Kxx=Kyy=431.5 MN/m Note: The sum of shear forces in each direction shall be equal to the corresponding seismic force, regardless of the stiffness distribution or the deviation of the CM from the CT, i.e. in this particular caseΣ(Vx)=2000 kN and Σ(Vy)=0 |