Effective width of flanges [EC2 A§5.3.2.1]
Τhe effective flange width beff depends on the distance lo between consecutive zero moment points and on half the spans b1, b2 at both sides of slabs.
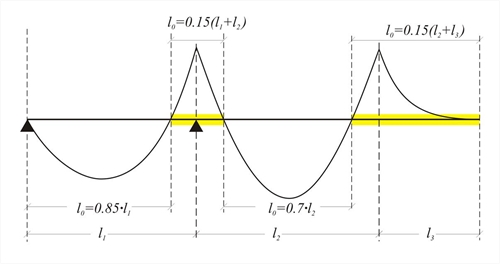 Figure 3.1.2-1: Continuous beam: lo distance between consecutive points of zero moments
Figure 3.1.2-1: Continuous beam: lo distance between consecutive points of zero moments Figure 3.1.2-1: Continuous beam: lo distance between consecutive points of zero moments
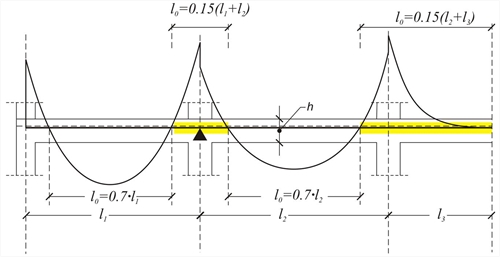 Figure 3.1.2-2: Continuous beam of frames: lo distance between consecutive points of zero moments
Figure 3.1.2-2: Continuous beam of frames: lo distance between consecutive points of zero moments Figure 3.1.2-2: Continuous beam of frames: lo distance between consecutive points of zero moments
Earthquake resistant structures require strong columns and fixed column-beam connections. This requirement demands the creation of a frame set of beams, forming a continuous structure with respect to geometry, but autonomous with respect to the adjacent beams. This fact leads to the conclusion that, in general, the supports of a beam are rarely hinged. Therefore, lo=0.70·l can be chosen for all the earthquake resistant beams.
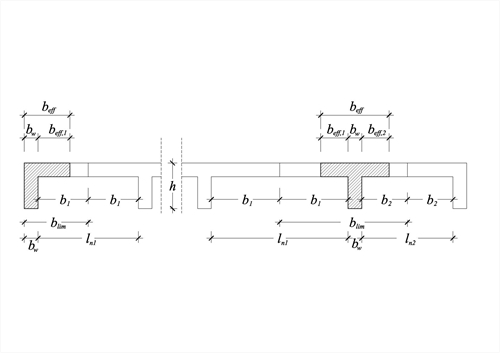 Figure 3.1.2-3
Figure 3.1.2-3 Figure 3.1.2-3
b eff =b w +b eff,1 +b eff,2 ≤b lim
where beff,1=0.20·b1+0.10·lo≤0.20·loandbeff,2=0.20·b2+0.10 ·lo≤0.20·lo.
-
Τhe effective widths at supports have practical meaning mainly for the dimensioning of inverted concrete beams under bending.
-
When an adjacent slab is cantilever, of a span ln, the corresponding b1ή b2 is equal to ln.
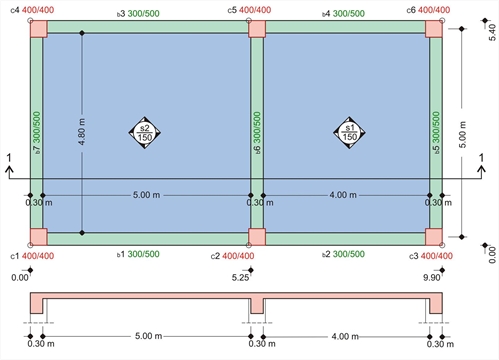 Figure 3.1.2-4: Woodwork plan and section 1-1
Figure 3.1.2-4: Woodwork plan and section 1-1 Figure 3.1.2-4: Woodwork plan and section 1-1
The end beam b5 has cross-section 300/5 and span l=5.00 m. The clear span on the left of slab s1 is ln1=4.00 m. The calculation of the effective flange width is requested.
lo=0.70·l=0.70x5.00=3.50 m
b1=ln1/2=4.00/2=2.00 m, blim=bw+b1=0.30+2.00=2.30 m
Τhe effective width is equal to:
beff=min(bw+beff,1, blim)=min(0.30+0.70, 2.30)=1.00 m
beff,1=min(0.20·b1+0.10·lo,0.20·lo)=min(0.20x2.00+0.10x3.50, 0.20x3.50)=min(0.75, 0.70)=0.70 m.
The middle beam b6 has the same dimensions as b5. The span of the slab on the left of b6 is ln1=5.00 m. The span of the slab on the right of b6 is ln2=4.00 m. The calculation of the effective flange width is requested.
This flange is of type T.
b1=ln1/2=5.00/2=2.50 m, b2=ln2/2=4.00/2=2.00 m, blim=bw+b1+b2 =0.30+2.50+2.00=4.80 m
Τhe effective width is equal to:
beff=min(bw+beff,1+beff,2, blim)=min(0.30+0.70+0.70, 4.80)=1.70 m
beff,2=0.70 m (same with beff,1 of beam b5)
beff,1=min(0.20·b1+0.10·lo,0.20·lo )=min(0.20x2.50+0.10x3.5,0.20x3.50)=min(0.85, 0.70)=0.70 m.