Bending moments in continuous two-way slabs|www.BuildingHow.com

VOLUME A
The art of construction and detailing
Introduction
The structural frame
- Introduction
- Structural frame elements
  - Columns
  - Beams
  - Slabs
  - Staircases
  - Foundation
- STRUCTURAL FRAME LOADING
- BEHAVIOR OF THE STRUCTURAL FRAME
  - The behavior and reinforcement of a slab
  - Behavior and reinforcement of beams and columns
Construction methods
- The materials
- The moulds
- Thermal insulation of structural elements
- Concrete
- The steel
- Reinforcement specifications of antiseismic design
- Industrial stirrups - stirrup cages
- Standardized cross-sections of reinforced concrete elements
Reinforcement
- Columns
- Shear walls
- Composite elements
- Beams
- Slabs
- Staircases
- Foundation
Quantity surveying
- Estimation of the concrete’s quantity
- Estimation of the formworks’ quantity
- Estimation of the spacers’ quantity
- Estimation of the reinforcements' quantity
- Total estimation of the materials’ quantities
- Optimization of the reinforcement schedule
- Estimation of the structural frame’s cost
- Electronic exchange of designs - bids - orders
Detailing drawings
- General
- The drawings’ title block
- Carpenter’s drawings
- Steel fixer’s drawings
Tables
- Table 1
- Table 2
- Table 3
Drawings
- Carpenter’s drawings
- Steel fixer’s drawings
Model (exemplary) construction

« Fundamental support and span moments - Deflection curves Influence of live load »

Bending moments in continuous two-way slabs

Continuous strip method

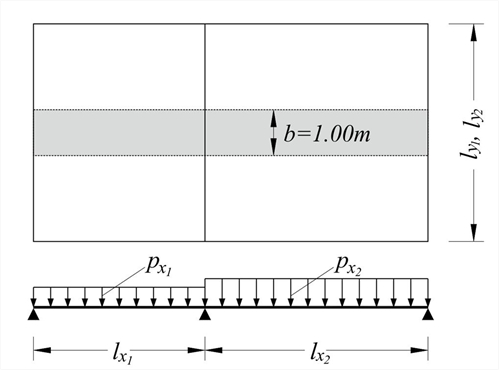Figure 4.6.3.1-1: Strips (zones) of 1.00 m width are considered along the directions of continuity

Strips are solved as continuous one-way slabs, with loads p_xi and p_yi applied on spans l_xi and l_yirespectively, using one of the known methods.

Stiffness coefficients are determined considering each strip as bar fixed either at one or both ends.

The errors associated with the calculations of stiffness by this method could be very significant, due to considering the strips as independent bars. In reality, the stiffness of slab depends on both directions.

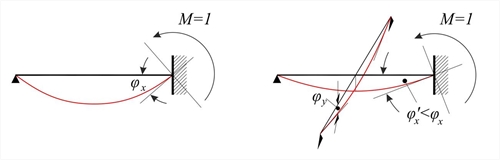Figure 4.6.3.1-2: One-way and Two-way slab

Even greater error occurs in the calculation of transfer coefficients of support moments, as well as in the calculation of span moments, due to rotation of the support (or equivalently, due to external moment imposed on the support).

These differences are shown in the next example.

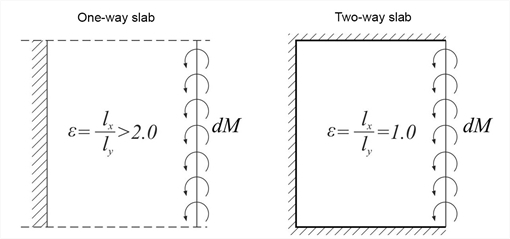Figure 4.6.3.1-4: Stiffness index K = I / (Ic Ix) (one way slab) and K = 1.875 I / (Ic Ix) (two way slab)

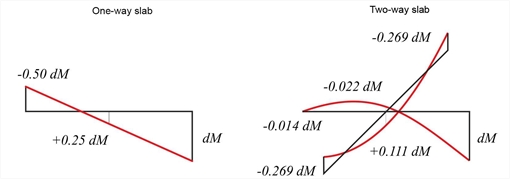Figure 4.6.3.1-6: Half of the transfer moment dM on the support of a one-way slab is shifted to the opposite support(left diagram).The same transfer moment dM on the support of a two-way slab is “diffused” all over its surface (right diagram)

Accurate method (manual)

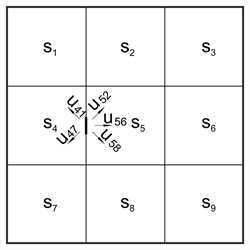Figure 4.6.3.2

Stiffness coefficients and transfer indices of each slab depend on its type of support and its aspect ratio. These data are provided by tables in several books, e.g. by Hahn.

All supports are considered fixed when principal moments are calculated.

One support is freed, e.g. 45 of the figure, and distribution takes place on all directions (i.e. CROSS method on plane).

This procedure is repeated until moments balance.

Such a solution is, certainly, complex and laborious, but it is applicable in case of large spans with significant differences in dimensions and thicknesses.

Practically accurate method

In usual cases of slabs with almost the same thickness (even for large or uneven spans), support moments are calculated with reasonable accuracy according to the expression:

are the principal moments at support 1.

Figure 4.6.3.3

Support moments affect at minimum level span moments, resulting the latter to be calculated considering rigid supports.

This particular method is applied in the majority of practical problems, as it combines adequate accuracy (much more accurate than the strip method) with high speed application.

« Fundamental support and span moments - Deflection curves Influence of live load »