The effect of torsional stiffness on indirect beam-to-beam supports The torsional stiffness of a supporting beam affects the degree of fixity of the beams supported (indirect beam-to-beam support). Structure I: Frame beam supported on bearing beam of another frame In project <B_334-1> of the related software, the supporting beam b1 has cross-section 300/500 and spanl1=4.0 m, whereas the supported beam b2 on b1 has identical cross-section 300/500 and span l2=5.0 m. 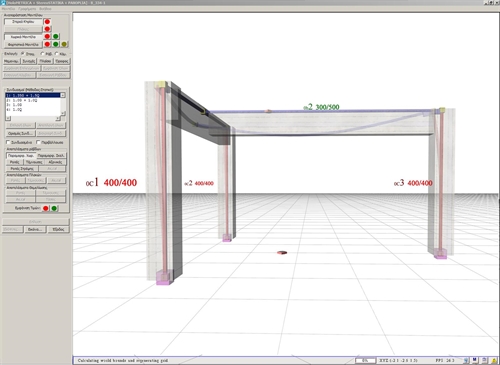 Figure 3.3.4-1: Displaced structure (ultimate limit state loads)
Figure 3.3.4-1: Displaced structure (ultimate limit state loads) Figure 3.3.4-1: Displaced structure (ultimate limit state loads) If the effective torsional stiffness of the supporting beam is taken equal to 100% of its corresponding full torsional elastic stiffness, then the bending moment of the left (indirect) support of the supported beam b2 is equal to M=-40.4 kNm.
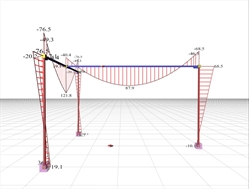 Figure 3.3.4-2: Bending moment diagrams of the structure (Effective torsional stiffness taken equal to 100% of the full elastic stiffness)
Figure 3.3.4-2: Bending moment diagrams of the structure (Effective torsional stiffness taken equal to 100% of the full elastic stiffness) Figure 3.3.4-2: Bending moment diagrams of the structure (Effective torsional stiffness taken equal to 100% of the full elastic stiffness) | 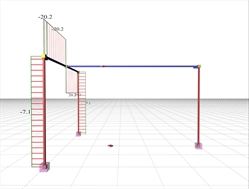 Figure 3.3.4-3: Torsional moment diagrams of the supporting beam (Effective torsional stiffness taken equal to the 100% of the full elastic stiffness)
Figure 3.3.4-3: Torsional moment diagrams of the supporting beam (Effective torsional stiffness taken equal to the 100% of the full elastic stiffness) Figure 3.3.4-3: Torsional moment diagrams of the supporting beam (Effective torsional stiffness taken equal to the 100% of the full elastic stiffness) |
At the left (indirect) support of the supported beam b2 the reinforcing bars, designed for bending moment M=-40.4 kNm should be placed at the top fibers and anchored inside the supported beam b1. In the span, the reinforcing bars, designed for bending moment M=87.9 kNm should be placed at the bottom fibers. The bending moment of the supported beam b2 transfers a torsional moment MT=M/2=40.4/2=20.2 kNm onto the supporting beam b1, as shown on the corresponding diagram of torsional moments. In conclusion, the supporting beam b1 should be designed for torsion. - If the supported beam b2 had cross-section 300/300, then the moment of the left (indirect) support of b2 would be equal to M=-65.3 kNm. Therefore the torsional moment of the supporting beam b1 would result to MT=65.3/2=32.7 kNm, while the moment in the span of b2 would be equal to M=56.2 kNm.
Provided that the structure is suitably reinforced and the formwork remains in place after concreting until the application of all design loads, when the formwork is dismantled, the static system will function according to the assumptions made during the calculations, i.e. elastically. Afterwards, beam b1 will start to behave plastically due to creep. The lack of negative reinforcement or its inappropriate anchorage contributes positively to the plasticity of beams. .jpg?bhow=0&w=500&h=500&Str=0) Figure 3.3.4-4: Torsional deformation of the supporting beam b1
Figure 3.3.4-4: Torsional deformation of the supporting beam b1 Figure 3.3.4-4: Torsional deformation of the supporting beam b1 The assumption of zero torsional stiffness provides a solution in the case of a simply supported beam. However, in the case of a cantilever beam, this turns out to be invalid, because the isostatic structure becomes a mechanism by diminishing its rotational restraint and thus transforming the support from fixed to hinged. .jpg?bhow=0&w=500&h=500&Str=0) Figure 3.3.4-6: Simply supported beam with one end supported on another beam(Effective torsional stiffness limited to 1% of the full elastic stiffness)
Figure 3.3.4-6: Simply supported beam with one end supported on another beam(Effective torsional stiffness limited to 1% of the full elastic stiffness) Figure 3.3.4-6: Simply supported beam with one end supported on another beam(Effective torsional stiffness limited to 1% of the full elastic stiffness) In the case of the simply supported beam b2, with an effective torsional stiffness 1% of the respective full elastic one, the indirect support of b2 on b1 practically behaves as hinged without transferring any torsional moment to the supported beam b1. The beam b2 should be designed only for bending moment M=110.9 kNm along its span, which is significantly greater than the moment 87.9 kNm of the previous case with an effective torsional stiffness equal to the full elastic one. The rotation angle of the supporting beam b1 in coordinate system xyz (φz,0) will be equal to the rotation angle of the supported beam b2 in coordinate system x'y'z' (φy',0), i.e. φz,0=φy',0. The rotation angle φz,t of the supporting beam b1 will be increasing over time t, due to creep. As φy',t=φz,t, the equivalent angle φy',t of the supported beam b2 will also be increasing. Consequently, the bending moment M and the equivalent torsional moment MT will be increasing, since MT=M. At time t=∞, the system will balance at an angle φy', ?=φz, ?, which cannot exceed the angle φy',hinged. The φy',hinged corresponds to the tangent of the elastic line at the left end of the supported beam b2 when the support there becomes hinged (MT=M=0 [*] NoteThe same will occur if the reinforcement at the upper fibers of the support of b2 is not anchored properly inside b1, or if b1 is not reinforced adequately for torsion. ). NoteThe same will occur if the reinforcement at the upper fibers of the support of b2 is not anchored properly inside b1, or if b1 is not reinforced adequately for torsion. ). This is why the European Standards [EC2, §5.3.2.2(2)] allow us to consider hinged supports for both beams and slabs. Otherwise, either the creep should be taken into account or the effective stiffness should be limited to a small percentage (e.g. 10%) of the full elastic stiffness.
.jpg?bhow=0&w=500&h=500&Str=0) Figure 3.3.4-5: Detail of torsional deformation in the middle of the supporting beam b1 (cross-section Α-Α):
Figure 3.3.4-5: Detail of torsional deformation in the middle of the supporting beam b1 (cross-section Α-Α):
φz,0: the elastic angular deformation at time t=0
φz,∞: the elastic angular deformation at time t=∞ Figure 3.3.4-5: Detail of torsional deformation in the middle of the supporting beam b1 (cross-section Α-Α):
φz,0: the elastic angular deformation at time t=0
φz,∞: the elastic angular deformation at time t=∞
Structure II: Cantilever beam supported on bearing beam of the frame  Figure 3.3.4-7: Effective torsional stiffness equal to 1% of the elastic stiffness, project <B_334-2> (1)bending moment, (2)torsional moment
Figure 3.3.4-7: Effective torsional stiffness equal to 1% of the elastic stiffness, project <B_334-2> (1)bending moment, (2)torsional moment Figure 3.3.4-7: Effective torsional stiffness equal to 1% of the elastic stiffness, project <B_334-2> (1)bending moment, (2)torsional moment The support of the cantilever beam, on the bearing beam of the frame, behaves as fully restrained and transfers the moment of the support ( -64.1 kNm) as a torsional moment to the bearing beam. In an isostatic structure with respect to torsion, such as structure II, no matter how small the torsional stiffness of the bearing beam is, the torsional moments remain intact. -
In general, the torsional stiffness of beams should be considered insignificant at least on site-casting. -
Similar functionality is also provided for the slab-to-beam support as shown in the next paragraph.
|