|
« Assumptions
Cantilevers »
|
Support moments of continuous slabs 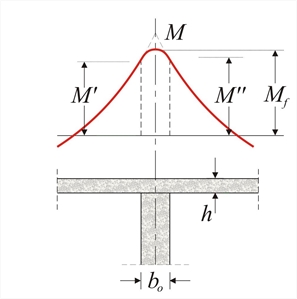 Figure 4.3.4-1
Figure 4.3.4-1 Figure 4.3.4-1
where V is the design support reaction. In monolithic supports of continuous slabs, as usually constructed in practice, the moments Μ', Μ'' at the two sides are:
(Μ, V in absolute values) or approximately M'=M''=0.90·M.
The moments Μ', Μ'' at the two sides should be greater than 0.65 of the principal moments Mo,l and Mo,r of the corresponding slab with fully fixed ends. 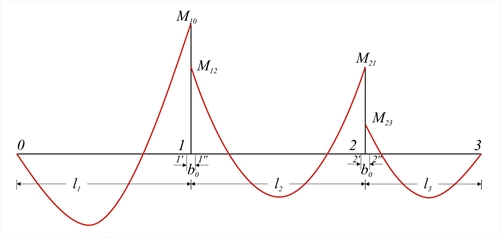 Figure 4.3.4-2: The principal moments, under uniform loads, are equal to M10=p1l12/8, M12=M 21=p2l22/12, M23= p3l32/8.
Figure 4.3.4-2: The principal moments, under uniform loads, are equal to M10=p1l12/8, M12=M 21=p2l22/12, M23= p3l32/8. Figure 4.3.4-2: The principal moments, under uniform loads, are equal to M10=p1l12/8, M12=M 21=p2l22/12, M23= p3l32/8.
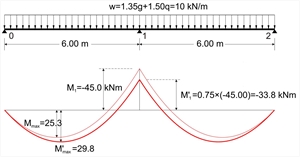 Figure 4.3.4-3: Moments redistribution example in 25%
Figure 4.3.4-3: Moments redistribution example in 25% Figure 4.3.4-3: Moments redistribution example in 25% In continuous slabs, support moments are allowed to be decreased [EC2, §5.5(4)] up to 30% when reinforcing steel of B or C category is used and up to 20% when reinforcing steel of A category is used, provided the increment of the respective span moments. This redistribution allows the required thickness due to bending to be decreased, while the simultaneous increment of the reinforcement is relatively small. For support moment Μ1=-45.0 kNm, shear force is V0=10.0x6.00/2-45.0/6.00=22.5 kN and zero shear point (maximum moment point, see §3.3.3, sub note 10) is positioned at x=22.5/10.0=2.25 m. The maximum span moment at this point is Mmax=V0·x/2=22.5x2.25/2=25.3 kNm. Reducing support moment Μ1 by 25%, we have: V'0=10.0x6.00/2-33.8/6.00=24.4 kN M'max=V'0·x'/2=24.4x2.44/2=29.8 kNm Note that the span moment is increased by (29.8-25.3)/25.3=18%. Contribution of pinned slab supports Elastic analysis and use of table for two-way slabs, assume that corners are prevented from lifting and that diagonal twisting moments at those corners are carried by longitudinal reinforcement grid in upper and lower fibres. These two structural conditions are satisfied in practice, since reinforcement of slabs interlace with stirrups and longitudinal reinforcement of beams, thus preventing the lift of corners and creating a reinforcement grid in upper and lower fibres of the corners. Where (mandatory) construction standards (see volume Α' §3.5) are not fully satisfied, although the equilibrium conditions will be met for the slabs, the span moments should increase by 5% - 33%. |
« Assumptions
Cantilevers »
|

|