Two-way slabs|Shear forces and support reaction forces|

VOLUME A
The art of construction and detailing
Introduction
The structural frame
- Introduction
- Structural frame elements
  - Columns
  - Beams
  - Slabs
  - Staircases
  - Foundation
- STRUCTURAL FRAME LOADING
- BEHAVIOR OF THE STRUCTURAL FRAME
  - The behavior and reinforcement of a slab
  - Behavior and reinforcement of beams and columns
Construction methods
- The materials
- The moulds
- Thermal insulation of structural elements
- Concrete
- The steel
- Reinforcement specifications of antiseismic design
- Industrial stirrups - stirrup cages
- Standardized cross-sections of reinforced concrete elements
Reinforcement
- Columns
- Shear walls
- Composite elements
- Beams
- Slabs
- Staircases
- Foundation
Quantity surveying
- Estimation of the concrete’s quantity
- Estimation of the formworks’ quantity
- Estimation of the spacers’ quantity
- Estimation of the reinforcements' quantity
- Total estimation of the materials’ quantities
- Optimization of the reinforcement schedule
- Estimation of the structural frame’s cost
- Electronic exchange of designs - bids - orders
Detailing drawings
- General
- The drawings’ title block
- Carpenter’s drawings
- Steel fixer’s drawings
Tables
- Table 1
- Table 2
- Table 3
Drawings
- Carpenter’s drawings
- Steel fixer’s drawings
Model (exemplary) construction

« Effect of live load on the static analysis of one-way slabs Fundamental support and span moments - Deflection curves »

Two-way slabs

Shear forces and support reaction forces

A slab supported on all four edges with an aspect ratio of longer to shorter theoretical span less than ≤2.00, is considered to be two-way.

Static analysis of two-way slabs, subjected to uniform load, is performed using tables, which give the fundamental support moments, span moments and shear forces.

In these tables, each slab is characterized by a number from 1 to 6, depending on the type of support, as illustrated in the following figure: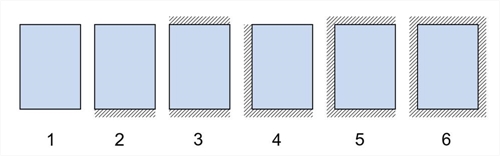

Figure 4.6

The floor diaphragm, as a rule, consists of many connected slabs affecting each other. The accurate calculation of these influences is performed only by means of two dimensional finite elements. In usual cases, shear and reaction forces are not affected by adjacent slabs. An additional reason for considering slabs isolated, is to use simplified methods for the calculation.

Simplified method

Distribution of load is considered as triangular or trapezoidal. Heights of triangles/trapezoids determine the maximum values of load transferred to the corresponding points of the peripheral support. These maximum loads are the maximum shear forces V_i,j of the slab, while equivalent loads p _i,j represent the equivalent uniform reactions.

The distribution of reaction forces may be calculated according to the following simplified rule: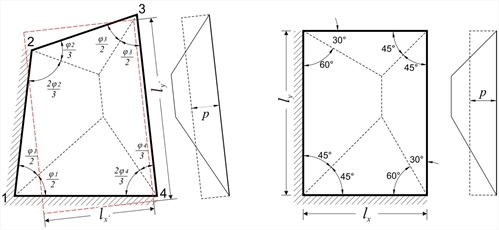

Figure 4.6.1.1-1

At the intersection of two similar edges (both fixed and simply supported) load is distributed with sharing angle φ/2 (45^ο for rectangular slab).
· At the intersection of two dissimilar edges (one fixed and the other simply supported), load is distributed with sharing angle 2φ/3 towards the fixed edge (60º for rectangular slab) and φ/3 towards the simply supported edge (30º for rectangular slab).

Notes:

In the example presented in the previous figure, the equivalent rectangular slab is indicated by a red dashed line. Dimensions l_x', l _y'are determined bu considering equal area and moments of inertia.
The above rule for the load distribution is also valid for slabs with more than four edges.
The load distribution rule adopted approximates the accurate one according to elasticity theory. In practice, trapezoidal loading represented by equivalent rectangular, as shown in the following figures.
Supports which are not taken into account in the calculation of a slab, should participate in the load distribution.
The same approach may be applied to slabs supported on two or three edges.

The values of coefficients of shear forces V_i,j and equivalent uniform reactions p_i,j are given in the six tables b5.1 to b5.6 cite in the end of the book.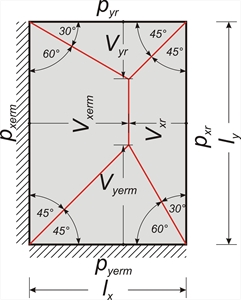

Figure 4.6.1.1-2

V_xr=ρ_xr·p·l_x

V_xerm=ρ_xerm·p·l_x

V_yr= ρ_yr·p·l_x

V_yerm= ρ_yerm·p·l_x

p_xr=υ_xr·p·l_x

p_xerm=υ_xerm·p·l_x

p_yr= υ_yr·p·l_x

p_yerm= υ_yerm·p·l_x

In each of six support cases two triangles and trapezoids are formed in directions x, y or conversely (depending on the side ratio).

Next, the general case of slabs is considered for two aspect ratios where S≥0 (as shown in the two following figures). Tables b5 have been composed according to the resulting equations.

General simplified calculation of shear forces and reaction forces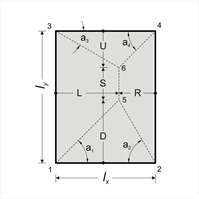

Figure 4.6.1.1-3

V_L=L·p=ρ_L·p·l_x, V_R=R·p=ρ_R·p·l_x, V_D=D·p=ρ_D·p·l_x, V_U=U·p=ρ_U·p·l_x

p_L=(A_1,3,6,5·p)/l_y=υ_L·p·l_x

p_R=(A_2,4,6,5·p)/l_y=υ_R·p·l_x, p_D=(A_1,2,5·p)/l_x=υ_D·p·l_x

p_U=(A_3,4,6·p)/l_x=υ_U·p·l_x

Figure 4.6.1.1-4

V_L=L·p=ρ_L·p·l_x, V_R=R·p=ρ_R·p·l_x, V_D=D·p=ρ_D·p·l_x, V_U=U·p=ρ_U·p·l_x

p_L=(A_1,3,5·p)/l_y=υ_L·p·l_x

p_R=(A_2,4,6·p)/l_y=υ_R·p·l_x, p_D=(A_1,2,6,5·p)/l_x=υ_D·p·l_x

p_U=(A_3,4,6,5)·p/l_x=υ_U·p·l_x

D=[1/(cota₁+cota₂)]·l_x=ρ_D·l_x , where ρ_D=1/(cota₁+cota₂)

U=[1//(cota₃+cota₄)]·l_x=ρ_U·l_x , where ρ_U=1/(cota₃+cota₄)

L=[cota₁/(cota₁+cota₂)]·l_x=ρ_L·l_x , where ρ_L=cota₁/(cota₁+cota₂)

R=[cota₂/(cota₁+cota₂)]·l_x=ρ_R·l_x , where ρ_R=cota₂/(cota₁+cota₂)

S=l_y-D-U=(ε-ρ_D-ρ_U)·l_x

p_L=A_1,3,6,5/l_y=0.50·(l_y+S)·L/(ε·l_x)=0.50·(2ε-ρ_D-ρ_U)·ρ_L·l_x·l_x/(ε·l_x)=υ_L·p·l_x , where υ_L=[0.50·(2ε-ρ_D-ρ_U)·ρ_L]/ε

p_R=A_2,4,6,5/l_y=0.50·(l_y+S)·R/(ε·l_x)=0.50·(2ε-ρ_D-ρ_U)·ρ_R·l_x·l_x/(ε·l_x)= =υ_R·p·l_x , where υ_R=[0.50·(2ε-ρ_D-ρ_U)·ρ_R]/ε

p_D=(A_1,2,5·p)/l_x=0.50·l_x·D/l_x=0.50·ρ_D·l_x , whereυ_D=0.50·ρ_D

p_U=(A_3,4,6·p)/l_x=0.50·l_x·U/l_x=0.50·ρ_U·l_x , where<υ_U=0.50·ρ_U

Verification: (α) S≥0, (b) L+R=l_x, (c) υ_L+υ_R+(υ_D+υ_U)/ε=1.0

Example: slab type 4, l_x=4.0 m, l_y=6.0 m, p=15.0 kN/m²

ε=l_y/l_x=6.0/4.0=1.5. For slab type 4 a₁=45°, a₂=60°, a₃=30°, a₄=45°, thus

ρ_yerm=ρ_D=0.634, ρ_yr=ρ_U=0.366, ρ_xerm=ρ_L=0.634, ρ_xr=ρ_R=0.366 S=(1.5-0.634-0.366)·l_x=0.50·l_x

υ_xerm=υ_L=[0.50x(2x1.5-0.634-0.366) x0.634]/1.5=0.423

υ_xr=υ_R=[0.50x(2x1.5-0.634-0.366) x0.366]/1.5=0.244

υ_yerm=υ_D=0.50·ρ_D=0.50x0.634=0.317

υ_yr=υ_U=0.50·ρ_U=0.50x0.366=0.183

Consequently:

V_xerm=ρ_xerm·p·l_x=0.634x15.0x4.0=38.04 kN/m

V_xr= ρ_xr·p·l_x=0.366x15.0x4.0=21.96 kN/m

V_yerm= ρ_yerm·p·l_x=0.634x15.0x4.0=38.04 kN/m

V_yr= ρ_yr·p·l_x=0.366x15.0x4.0=21.96 kN/m

p_xerm=υ_xerm·p·l_x=0.423x15.0x4.0=25.38 kN/m

p_xr= υ_xr·p·l_x=0.244x15.0x4.0=14.64 kN/m

p_yerm= υ_yerm·p·l_x=0.317x15.0x4.0=19.02 kN/m

p_yr= υ_yr·p·l_x=0.183x15.0x4.0=10.98 kN/m

L=[1/(tana₁+tana₃)]·l_y=ρ_L·l_x, where ρ_L=ε/(tana₁+tana₃)

R=[1/(tana₂+tana₄)]·l_y=ρ_R·l_x, where ρ_R=ε/(tana₂+tana₄)

D=[tana₁/(tana₁+tana₃)]·l_y=ρ_D·l_x, where ρ_D=(ε·tana₁)/(tana₁+tana₃)

U=[tana₂/(tana₁+tana₃)]·l_y=ρ_U·l_x, where ρ_U=(ε·tana₃)/(tana₁+tana₃)

S=l_x-L-R=(1-ρ_L-ρ_R)·l_x

p_L=(A_1,3,5·p)/l_y=0.50·l_y·L/l_y=0.50·ρ_L·l_x, where υ_L=0.50·ρ_L

p_R=(A_2,4,6·p)/l_x=0.50·l_y·R/l_y=0.50·ρ_U·l_x, where υ_R=0.50·ρ_R

p_D=A_1,2,6,5/l_x=0.50·(l_x+S)·D/l_x=0.50 · (2-ρ_L-ρ_R)·ρ_D·l_x·l_x/l_x=υ_D·p·l_x,where υ_D=0.50·(2-ρ_L-ρ_R)·ρ_D

p_U=A_3,4,6,5/l_x=0.50·(l_x+S)·U/l_x=0.50 · (2-ρ_L-ρ_R)·ρ_U·l_x·l_x/l_x=υ_U·p·l_x,

where υ_U=0.50·(2-ρ_L-ρ_R)·ρ_U

Verification: (a) S≥0, (b) D+U=ε·l_x, (c) υ_L+υ_R+(υ_D+υ_U)/ε=1.0

Example: slab type 4, l_x=6.0 m, l_y=4.0 m, p=15.0 kN/m²

ε=l_y/l_x=4.0/6.0=2/3. For slab type 4 a₁=45°, a₂=60°, a₃=30°, a₄=45°, thus

ρ_xerm=ρ_L=0.423, ρ_xr=ρ_R=0.244, ρ_yerm=ρ_D=0.423, ρ_yr=ρ_U=0.244, S=(1-0.423-0.244)·l_x=0.333·l_x

υ_xerm=υ_L=0.50·ρ_L=0.50x0.423=0.212

υ_xr=υ_R=0.50·ρ_R=0.50x0.244=0.122

υ_yerm=υ_D=0.50x(2-0.423-0.244)x0.423=0.282

υ_yr=υ_U=0.50x(2-0.423-0.244)x0.244=0.163

Consequently:

V_xerm=ρ_xerm·p·l_x=0.423x15.0x6.0=38.07 kN/m

V_xr=ρ_xr·p·l_x=0.244x15.0x6.0=21.96 kN/m

V_yerm= ρ_yerm·p·l_x=0.423x15.0x6.0=38.07 kN/m

V_yr= ρ_yr·p·l_x=0.244x15.0x6.0=21.96 kN/m

p_xerm=υ_xerm·p·l_x=0.212x15.0x6.0=19.08 kN/m

p_xr= υ_xr·p·l_x=0.122x15.0x6.0=10.98

p_yerm=υ_yerm·p·l_x=0.282x15.0x6.0=25.38 kN/m

p_yr= υ_yr·p·l_x=0.163x15.0x6.0=14.67 kN/m

Czerny's elasticity method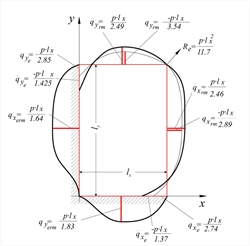

Figure 4.6.1.2-1: Shear force diagram by Czerny for side
ratio 1.50

According to the theory of elasticity, the distribution of shear forces along the length of the four edges of a slab, results from the shear forces along its perimeter as described by equations. The most unfavourable shear forces along the sides of a slab (as well as the most unfavourable bending moments) are tabulated in the tables of the book entitled "Applications of Reinforced Concrete" (p46-51 for two-way slabs, p52-59 three- or two-side-supported slabs) of series of books by Apostolos Konstantinidis published in1994.

Figure 4.6.1.2-2

Depending on the ε = l_x / l_y (where l_x is the shortest dimension) and the type of support, shear forces at the edges are equal to:

Notes:

The simplified method produces more unfavourable shear forces than the previously reported tables.
Both the elasticity equations and the corresponding tables, refer to orthogonal slabs or symmetric combinations of them. The general solution taking into account various shapes and arbitrary arrangement of slabs is obtained accurately only by means of the finite element method.

« Effect of live load on the static analysis of one-way slabs Fundamental support and span moments - Deflection curves »