Exercise 4.9.3|www.BuildingHow.com

VOLUME A
The art of construction and detailing
Introduction
The structural frame
- Introduction
- Structural frame elements
  - Columns
  - Beams
  - Slabs
  - Staircases
  - Foundation
- STRUCTURAL FRAME LOADING
- BEHAVIOR OF THE STRUCTURAL FRAME
  - The behavior and reinforcement of a slab
  - Behavior and reinforcement of beams and columns
Construction methods
- The materials
- The moulds
- Thermal insulation of structural elements
- Concrete
- The steel
- Reinforcement specifications of antiseismic design
- Industrial stirrups - stirrup cages
- Standardized cross-sections of reinforced concrete elements
Reinforcement
- Columns
- Shear walls
- Composite elements
- Beams
- Slabs
- Staircases
- Foundation
Quantity surveying
- Estimation of the concrete’s quantity
- Estimation of the formworks’ quantity
- Estimation of the spacers’ quantity
- Estimation of the reinforcements' quantity
- Total estimation of the materials’ quantities
- Optimization of the reinforcement schedule
- Estimation of the structural frame’s cost
- Electronic exchange of designs - bids - orders
Detailing drawings
- General
- The drawings’ title block
- Carpenter’s drawings
- Steel fixer’s drawings
Tables
- Table 1
- Table 2
- Table 3
Drawings
- Carpenter’s drawings
- Steel fixer’s drawings
Model (exemplary) construction

« Exercise 4.9.2 Exercise 4.9.4 »

Exercise 4.9.3

Given : Covering load g_e=1.00 kN/m², live loads of domestic use q₁=q₂=2.00 kN/m², q₃=5.00 kN/m², concentrated load applied at the free end of the cantilever G₃=1.00 kN/m.

Question : Perform static analysis for the slabs illustrated in the figure (a) under global loading and (b) taking into account the effect of live loads.

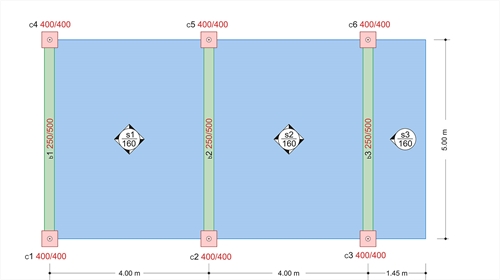Figure 4.9.3-1: Project <Β_49-3>

Solution:

Self-weight: g_o=0.16m·25.0kN/m³=4.00 kN/m²

Covering load: g_e= 1.00 kN/m²

Total dead load: g= 5.00 kN/m²

In ULS, the minimum design load for each slab i is equal to g_d,i=1.00·g, whereas the total design load is equal to p_d,i=γ_g·g_i+γ_q·q_i. In this case g_d,i=1.00x5.00=5.0 kN/m and G_d,3=1.00x1.0 kN (concentrated load). The maximum design load for the first two slabs is equal to p_d,1=p_d,2=1.35x5.00+1.50x2.00=9.75 kN/m, while for the third slab (balcony) is equal to p_d,3=1.35x5.00+1.50x5.00=14.25 kN/m και P_d,3=1.35x1.00=1.35 kN.

(A) Global loading

ULS design load is applied simultaneously on each slab.

Figure 4.9.3-2

(B) Unfavourable loadings

Figure 4.9.3-3

For this particular structure, the following six [*] Note NoteDue to the last bar 23 being a cantilever, if only bending moment envelope and not shear forces envelope is of interest, 4th and 6th loading could be omitted. unfavourable loadings cases are required.

For each loading case the expressions giving the solution are identical:

M₁₀=-p₁·l₀₁²/8

M₂=-p₃·l₂₃²/2-P₃ · l₂₃

M₁₂=-p₂·l₁₂²/8-M₂/2

M₁=(M₁₀+M₁₂)/2

V₀₁=p₁·l₀₁/2+M₁/l₀₁

V₁₀=-p₁·l₀₁/2+M₁/l₀₁

V₁₂=p₂·l₁₂/2+(M₂-M₁)/l₁₂

V₂₁=-p₂·l₁₂/2+(M₂-M₁)/l₁₂

V₂₃=p₃·l₂₃+P₃, V₃₂=P₃

maxM₀₁=V₀₁²/(2·p₁)

maxM₁₂=V₁₂²/(2·p₂)+M₁

GLOBAL LOADING ANALYSIS

Figure 4.9.3-4

M₁₀=-p₁·l₀₁²/8=-9.75x4.0²/8=-19.50 kNm

M₂=-p₃·l₂₃²/2-P₃·l₂₃=-14.25x1.45²/2-1.35x1.45=-16.94 kNm

M₁₂=-p₂·l₁₂²/8-M₂/2=-9.75x4.0²/8+16.94/2=-11.03 kNm

M₁=(M₁₀+M₁₂)/2=-(19.50+11.03)/2=-15.27 kNm

V₀₁=p₁·l₀₁/2+M₁/l₀₁=9.75x4.0/2-15.27/4.0=19.50-3.82=15.68 kN

V₁₀=-p₁·l₀₁/2+M₁/l₀₁=-9.75x4.0/2-15.27/4.0=-19.5-3.82=-23.32 kN

V₁₂=p₂·l₁₂/2+(M₂-M₁)/l₁₂=9.75x4.0/2+(-16.94+15.27)/4.0=19.50-0.42=19.08 kN

V₂₁=-p₂·l₁₂/2+(M₂-M₁)/l₁₂=-9.75 x4.0/2+ (-16.94+15.27)/4.0=-19.50-0.42=-19.92 kN

V₂₃=p₃·l₂₃+P₃=14.25 x1.45+1.35=20.66+ 1.35=22.01 kN, V₃₂=P₃=1.35 kN

maxM₀₁=V₀₁²/(2·p₁)=15.68²/(2x9.75)=12.61 kNm, maxM₁₂=V₁₂²/(2·p₂)+M₁= 19.08²/(2x9.75)-15.27=3.40 kNm

UNFAVOURABLE LOADINGS ANALYSIS

1^st loading case : maxΜ₀₁, minM₁₂

Figure 4.9.3-5

M₁₀=-p₁·l₀₁²/8=9.75x4.0²/8=-19.50 kNm

M₂=-p₃·l₂₃²/2-P₃·l₂₃=-14.25x1.45²/2-1.35x1.45=-16.94 kNm

M₁₂=-p₂·l₁₂²/8-M₂/2=-5.00x4.0²/8+16.94/2=-1.53 kNm

M₁=(M₁₀+M₁₂)/2=-(19.50+1.53)/2=-10.52 kNm

V₀₁=p₁·l₀₁/2+M₁/l₀₁=9.75x4.0/2-10.52/4.0=19.50-2.63=16.87 kN

V₁₀=-p₁·l₀₁/2+M₁/l₀₁=-9.75x4.0/2- 10.52/4.0=-19.50-2.63=-22.13 kN

V₁₂=p₂·l₁₂/2+(M₂-M₁)/l₁₂=5.00x4.0/2+ (-16.94+10.52)/4.0=10.00-1.61=8.39 kN

V₂₁=-p₂·l₁₂/2+(M₂-M₁)/l₁₂=-5.00x4.0/2+ (-16.94+10.52)/4.0=-10.00-1.61=-11.61 kN

V₂₃=p₃·l₂₃+P₃=14.25x1.45+1.35=20.66+1.35=22.01 kN, V₃₂=P₃=1.35 kN

maxM₀₁=V₀₁²/(2·p₁)=16.87²/(2x9.75)= 14.59 kNm

maxM₁₂=V₁₂²/(2·p₂)+M₁=8.39²/(2x5.00 )-10.52=-3.48 kNm

2^nd loading case : minM₀₁, maxM₁₂

Figure 4.9.3-6

M₁₀=-p₁·l₀₁²/8=-5.0x4.0²/8=-10.00 kNm

M₂=-p₃·l₂₃²/2-P₃ · l₂₃=-5.00x1.45²/2-1.00x1.45=-6.71 kNm

M₁₂=-p₂·l₁₂²/8-M₂/2=-9.75x4.0²/8+6.71/2=-16.15 kNm

M₁=(M₁₀+M₁₂)/2=-(10.00+16.15)/2=-13.07 kNm

V₀₁=p₁·l₀₁/2+M₁/l₀₁=5.00x4.0/2- 13.07/4.0=10.00-3.27=6.73 kN

V₁₀=-p₁·l₀₁/2+M₁/l₀₁=-5.00x4.0/2-13.07/4.0=-10.0-3.27=-13.27

V₁₂=p₂·l₁₂/2+(M₂-M₁)/l₁₂=9.75x4.0/2+(-6.71+13.07)/4.0=19.50+1.59=21.09 kN

V₂₁=-p₂·l₁₂/2+(M₂-M₁)/l₁₂=-9.75x4.0/2+(-6.71+13.07)/4.0=-19.50+1.59=-17.91 kN

V₂₃=p₃·l₂₃+P₃=5.00x1.45+1.00=8.25 kN V₃₂=P₃=1.00 kN

maxM₀₁=V₀₁²/(2·p₁)=6.73²/(2x5.00)=4.53 kNm

maxM₁₂=V₁₂²/(2·p₂)+M₁=21.09²/(2x9.75 )- 13.07=9.74 kNm

3^rd loading case : minM₁

Figure 4.9.3-7

M₁₀=-p₁·l₀₁²/8=-9.75x4.0²/8=-19.50 kNm

M₂=-p₃·l₂₃²/2-P₃·l₂₃=-5.00x1.45²/2-1.00x1.45=-6.71 kNm

M₁₂=-p₂·l₁₂²/8-M₂/2=-9.75x4.0²/8+6.71/2=-16.15 kNm

M₁=(M₁₀+M₁₂)/2=-(19.50+16.15)/2=-17.82 kNm

V₀₁=p₁·l₀₁/2+M₁/l₀₁=9.75x4.0/2-17.82/4.0=19.50-4.45=15.05 kN

V₁₀=-p₁·l₀₁/2+M₁/l₀₁=-9.75x4.0/2-17.82/4.0=-19.5-4.45=-23.95

V₁₂=p₂·l₁₂/2+(M₂-M₁)/l₁₂=9.75x4.0/2+(-6.71+17.82)/4.0=19.50+2.78=22.28 kN

V₂₁=-p₂·l₁₂/2+(M₂-M₁)/l₁₂=-9.75x4.0/2+(-6.71+17.82)/4.0=-19.50+2.78=-16.72 kN

V₂₃=p₃·l₂₃+P₃=5.00x1.45+1.00=8.25 kN V₃₂=P₃=1.00 kN

maxM₀₁=V₀₁²/(2·p₁)=15.05²/(2x9.75)=11.62 kNm

maxM₁₂=V₁₂²/(2·p₂)+M₁=22.28²/(2x9.75 )- -17.82=7.63 kNm

4^th loading case : minM₂

Figure 4.9.3-8

M₁₀=-p₁·l₀₁²/8=-5.0x4.0²/8=-10.00 kNm

M₂=-p₃·l₂₃²/2-P₃ · l₂₃=-14.25x1.45²/2-1.35x1.45=-16.94 kNm

M₁₂=-p₂·l₁₂²/8-M₂/2=-9.75x4.0²/8 +16.94/2=-11.03 kNm

M₁=(M₁₀+M₁₂)/2=-(10.00+11.03)/2=-10.52 kNm

V₀₁=p₁·l₀₁/2+M₁/l₀₁=5.00x4.0/2-10.52/4.0=10.00-2.63=7.37 kN

V₁₀=-p₁·l₀₁/2+M₁/l₀₁=-5.00x4.0/2-10.52/4.0=-10.0-2.63=-12.63

V₁₂=p₂·l₁₂/2+(M₂-M₁)/l₁₂=9.75x4.0/2+(-16.94+10.52)/4.0=19.50-1.61=17.89 kN

V₂₁=-p₂·l₁₂/2+(M₂-M₁)/l₁₂=-9.75x4.0/2+(-16.94+10.52)/4.0=-19.50-1.61=-21.11 kN

V₂₃=p₃·l₂₃+P₃=14.25x1.45+1.35=20.66+1.35=22.01 kN, V₃₂=P₃=1.35 kN

maxM₀₁=V₀₁²/(2 · p₁)=7.37²/(2x5.00)=5.43 kNm

maxM₁₂=V₁₂²/(2·p₂)+M₁=17.89²/(2x9.75)-10.52=5.89 kNm

5^th loading case : maxΜ₁

Figure 4.9.3-9

M₁₀=-p₁·l₀₁²/8=-5.0x4.0²/8=-10.00 kNm

M₂=-p₃·l₂₃²/2-P₃ · l₂₃=-14.25x1.45²/2-1.35x1.45=-16.94 kNm

M₁₂=-p₂·l₁₂²/8-M₂/2=-5.0x4.0²/8+16.94/2=-1.53 kNm

M₁=(M₁₀+M₁₂)/2=-(10.00+1.53)/2=-5.77 kNm

V₀₁=p₁·l₀₁/2+M₁/l₀₁=5.0x4.0/2-5.77/4.0=10.00-1.44=8.56 kN

V₁₀=-p₁·l₀₁/2+M₁/l₀₁=-5.0x4.0/2-5.77/4.0=-10.00-1.44=-11.44

V₁₂=p₂·l₁₂/2+(M₂-M₁)/l₁₂=5.0x4.0/2+(-16.94+5.77)/4.0=10.0-2.79=7.21 kN

V₂₁=-p₂·l₁₂/2+(M₂-M₁)/l₁₂=-5.0x4.0/2+(-16.94+5.77)/4.0=-10.0-2.79=-12.79 kN

V₂₃=p₃·l₂₃+P₃=14.25x1.45+1.35=20.66+1.35=22.01 kN, V₃₂=P₃=1.35 kN

maxM₀₁=V₀₁²/(2·p₁)=8.56²/(2x5.00)=7.33 kNm

maxM₁₂=V₁₂²/(2·p₂)+M₁=7.21²/(2x5.0 )-5.77=-0.57 kNm

6^th loading case : max M₂

Figure 4.9.3-10

M₁₀=-p₁·l₀₁²/8=-9.75x4.0²/8=-19.50 kNm

M₂=-p₃·l₂₃²/2-P₃ · l₂₃=-5.00x1.45²/2-1.00x1.45=-6.71 kNm

M₁₂=-p₂·l₁₂²/8-M₂/2=-5.00x4.0²/8+6.71/2=-6.64 kNm

M₁=(M₁₀+M₁₂)/2=-(19.50+6.64)/2= -13.07 kNm

V₀₁=p₁·l₀₁/2+M₁/l₀₁=9.75x4.0/2-13.07/4.0=19.50-3.27=16.23 kN

V₁₀=-p₁·l₀₁/2+M₁/l₀₁=-9.75x4.0/2-13.07/4.0=-19.5-3.27=-22.77

V₁₂=p₂·l₁₂/2+(M₂-M₁)/l₁₂=5.0x4.0/2+(-6.71+13.07)/4.0=10.00+1.59=11.59 kN

V₂₁=-p₂·l₁₂/2+(M₂-M₁)/l₁₂=-5.00x4.0/2+(-6.71+13.07)/4.0=-10.00+1.59=-8.41 kN

V₂₃=p₃·l₂₃+P₃=5.00x1.45+1.00=8.25 kN V₃₂=P₃=1.00 kN

maxM₀₁=V₀₁²/(2·p₁)=16.23²/(2x9.75)=13.51 kNm

maxM₁₂=V₁₂²/(2·p₂)+M₁=11.59²/(2x5.00 )- 13.07=0.36 kNm

ENVELOPE DIAGRAMS

Figure 4.9.3-11: The global loading diagram is illustrated with dashed line p_d=1.35xg+1.50xq

pi-FES (related software) produces the following diagrams:

Figure 4.9.3-12: Global loading,Shear force diagram (pi-FES)

Values through software calculations: 15.50 / -23.10 / 18.70 / -19.70 / 21.70

Values through manual calculations: 15.68 / -23.32 / 19.08 / -19.92 / 22.01

Figure 4.9.3-13: Global loading,Bending moment diagram (pi-FES)

Values through software calculations: 12.60 / -14.80 / 3.20 / -16.95

Values through manual calculations: 12.61 / -15.27 / 3.40 / -16.94

Figure 4.9.3-14: Unfavourable loadings,bending moment envelope (pi-FES)

Values through software calculations: 14.60 / -17.40 / 9.50 (-3.50) / -16.95

Values through manual calculations: 14.59 / -17.82 / 9.74 (-3.48) / -16.94

Figure 4.9.3-15: Unfavourable loadings,shear force envelope (pi-FES)

Values through software calculations: 16.60 / -23.70 / 21.90 / -20.70 / 21.70

Values through manual calculations: 16.87 / -23.95 / 22.98 / -21.11 / 22.01

Notes:

Although the two first slabs live load is small, the effect of the cantilever live load on the adjacent span is significant, altering its bending moment sign.
On the contrary, shear forces remain practically unaffected.
Standard Solver (related software) gives the following results:

Shear forces: 15.82 / -23.18 / 18.39 / -20.61 / 22.01, bending moments: 12.84 / -14.71 / 3.06 / -16.95

while manual calculations yield the following results:

Shear forces: 15.68 / -23.32 / 19.08 / -19.92 / 22.01, bending moments: 12.61 / -15.27 / 3.40 / -16.94

« Exercise 4.9.2 Exercise 4.9.4 »