Reinforced concrete structures have the capacity to dissipate energy, mainly by means of the ductile behaviour of their elements. The structural seismic response, which is reduced by the influence of ductility, is considered in the design spectrum for elastic analysis, according to the behaviour factor q.
The behaviour factor q depends on the structural type, the regularities in plan and elevation and the ductility class.
Structural types [EC8 §5.2.2.1]
Concrete buildings shall be classified into one of the following structural 6+1 types according to their behaviour under horizontal seismic actions.
Column is the vertical structural element of aspect ratio lw/hw≤4, while wall is the vertical structural element of aspect ratio lw/hw>4. In the building base, VF implies the seismic shear carried by all columns,VW the seismic shear carried by all walls and Vtot= VF + VW the total seismic shear at ground floor level.
Structural system comprising only columns, or both columns and walls, in which columns are the main resisting elements with VF/Vtot>0.65.
2. Ductile wall system (coupled or uncoupled)
Structural system comprising only walls, or both columns and walls, in which walls are the main resisting elements with VW/Vtot>0.65.
3. Frame-equivalent dual system
Structural system comprising both columns and walls with 0.50<VF/Vtot≤0.65.
4. Wall-equivalent dual system
Structural system comprising both columns and walls with 0.50<VW/Vtot≤0.65.
5. System of large lightly reinforced walls
System comprising at least two walls in the horizontal direction considered satisfying the three following conditions:
-
The horizontal dimension is lw≥min(4.0 m, 2hw/3),
-
The walls collectively support at least 20% of the total gravity load from above in the seismic design situation.
-
The fundamental period of the structure is ≤0.5 sec
If the first of the above conditions is satisfied but either the second or the third is not, then the system is classified as ductile wall system and all of its walls should be designed and detailed as ductile walls.
6. Inverted pendulum system
System in which 50% or more of the mass is in the upper third of the height of the structure.
One-storey frames with column tops connected along both main directions of the building and with the value of the column normalized axial load νd exceeding 0.3 nowhere, do not belong in this category.
7. Torsionally flexible system [EC8, 5.2.2.1(4)P]
.jpg?bhow=0&w=350&h=350&Str=0) Figure 6.1.5.1
Figure 6.1.5.1 Figure 6.1.5.1
Except for those classified as torsionally flexible systems, concrete buildings may be classified to different structural types in x and y horizontal directions.
Regularity in plan [EC8 §4.2.3.2]
For a building to be categorised as being regular in plan, it shall satisfy all the following conditions:
-
With respect to the lateral stiffness and mass distribution, the building structure shall be approximately symmetrical in plan with respect to two orthogonal axes.
Each floor shall be delimited by a polygonal convex line. If in plan set-backs exist, regularity in plan may still be considered as being satisfied, provided that these setbacks do not affect the floor in-plan stiffness. For each set-back, the area between the outline of the floor and a convex polygonal line enveloping the floor does not exceed 5 % of the floor area.
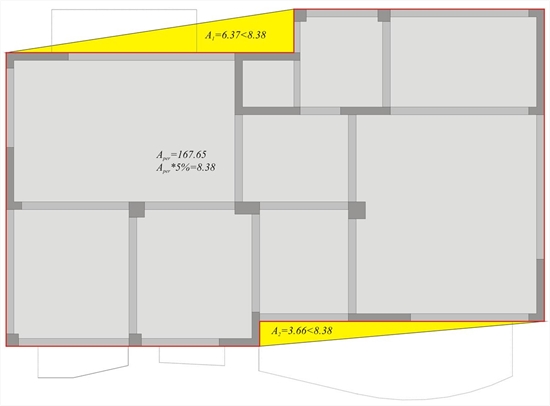 Figure 6.1.5.2
Figure 6.1.5.2 Figure 6.1.5.2
-
The in-plan stiffness of the floors shall be sufficiently large in comparison with the lateral stiffness of the vertical structural elements, in order to satisfy the rigid diaphragm condition. This condition is usually satisfied in reinforced concrete structures.
-
The slenderness λ of the building in plan shall be λ =Lmax/Lmin≤4
-
At each level shall be:
eox≤0.30rx & eoy≤0.30ry [provided is not flexible at the same time, i.e. min(rx, ry)≥ls ]
Consider eox=0.94 m≤0.30rx=0.30 · 3.91=1.17 m, but eoy=1.34 m>0.30ry=0.30 · 3.08=0.92 m which does not satisfy the necessary condition, thus the building comprising that specific floor is not considered as being regular in plan .
Regularity in elevation [EC8 §4.2.3.3]
For a building to be categorised as being regular in elevation, it shall satisfy all the following conditions:
i. All lateral load resisting systems, such as cores, structural walls, or frames, shall run without interruption from their foundations to the top of the building or, if setbacks at different heights are present, to the top of the relevant zone of the building. Cases of regular and non-regular in elevation buildings are presented in the following figures.
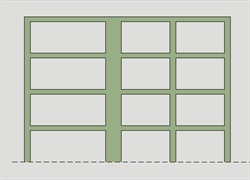 Figure 6.1.5.3-1: regular in elevation building
Figure 6.1.5.3-1: regular in elevation building Figure 6.1.5.3-1: regular in elevation building | 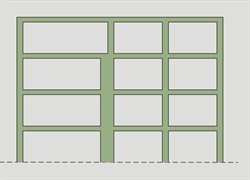 Figure 6.1.5.3-2: non-regular in elevation
Figure 6.1.5.3-2: non-regular in elevation
building (change of column dimension) Figure 6.1.5.3-2: non-regular in elevation
building (change of column dimension) |
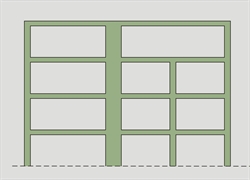 Figure 6.1.5.3-3: non-regular in elevation
Figure 6.1.5.3-3: non-regular in elevation
building(interrupted column) Figure 6.1.5.3-3: non-regular in elevation
building(interrupted column) | 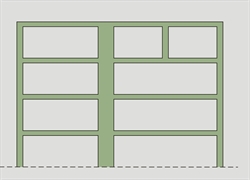 Figure 6.1.5.3-4: non-regular in elevation
Figure 6.1.5.3-4: non-regular in elevation
building(planted column) Figure 6.1.5.3-4: non-regular in elevation
building(planted column) |
 Figure 6.1.5.3-5: regular in elevation building
Figure 6.1.5.3-5: regular in elevation building
(column added of in the basement) Figure 6.1.5.3-5: regular in elevation building
(column added of in the basement) | 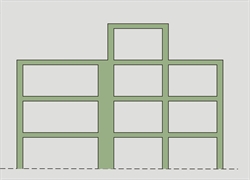 Figure 6.1.5.3-6: regular in elevation
Figure 6.1.5.3-6: regular in elevation
building(The top of the building does not
count as floor) Figure 6.1.5.3-6: regular in elevation
building(The top of the building does not
count as floor) |
ii.Both the lateral stiffness and the mass of the individual storeys shall remain constant or reduce gradually, without abrupt changes, from the base to the top of a particular building.The storey stiffness is defined as the ratio of the applied seismic force το the relative lateral stiffness (or equivalently, the displacement of the centre of stiffness).
The storey stiffness may be approximated by the sum all columns stiffnesses, i.e. Σ(E· I/h3).
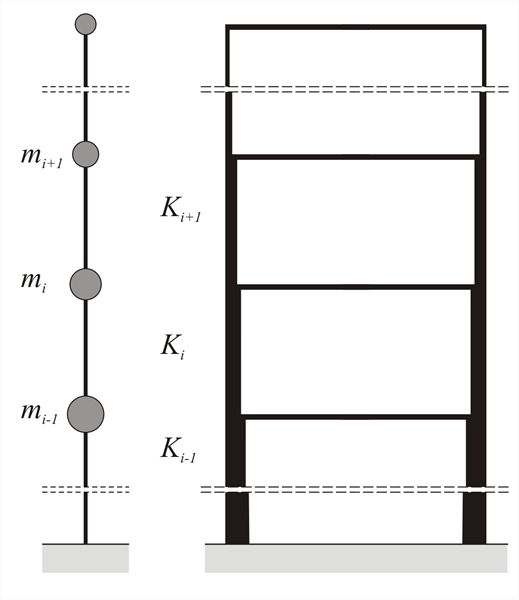 Figure 6.1.5.3-7: Change in mass and stiffness
Figure 6.1.5.3-7: Change in mass and stiffness Figure 6.1.5.3-7: Change in mass and stiffness
In the absence of particular data provided by the EC8, the limit values for the stiffness and mass fluctuation may be taken as being equal to:
Mass increase ΔMi=(Mi+1-Mi)≤0.35Mi,
Mass reduction ΔMi=(Mi-Mi+1)≤0.50Mi,
while for each main horizontal direction x, y
Relative stiffness increase
Δ Ki=(Ki+1-Ki)≤0.35Ki , Relative stiffness reduction
-
The stiffness ratio fluctuation is very sensitive. The most critical factor is the interstorey height since it is involved directly or non-directly in the calculation of the column stiffness raised in the 3rdpower. For instance, in case of two storeys with the same columns, the same loads and interstorey heights equal to 4.0 m and 3.0 m, respectively, the first is (4.0/3.0)3=2.4 times more flexible than the second and thus the building is considered as being non-regular in plan. For interstorey height 6.0 m, instead of 4.0 m, the corresponding ratio yields (6.0/3.0)3= 8. Such stories are called soft storeys having an unfavourable effect both on defining the building as being irregular in elevation, and on the stress and strain behaviour of the building.
-
Consider a building where two consecutive storeys have the same walls and frames but the first one has less slabs, e.g. as in mezzanines, then the second carries less loads than the first. That could affect the uniform mass distribution, resulting in the building being considered as non-regular in elevation.
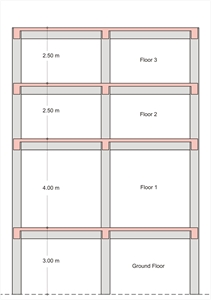 Figure 6.1.5.3-8: Non-regular in elevation,
Figure 6.1.5.3-8: Non-regular in elevation,
due to significant stiffness difference (soft storey) Figure 6.1.5.3-8: Non-regular in elevation,
due to significant stiffness difference (soft storey) | 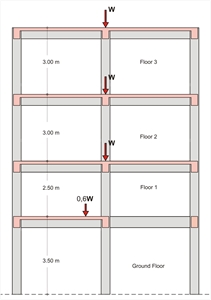 Figure 6.1.5.3-9: Non-regular in elevation,
Figure 6.1.5.3-9: Non-regular in elevation,
due to significant mass difference (loft) Figure 6.1.5.3-9: Non-regular in elevation,
due to significant mass difference (loft) |
iii. In framed buildings the ratio of the actual strength of columns and beams to the strength required by the analysis should not vary disproportionately from the corresponding overstrength factor between adjacent storeys. For each floor and each direction the column resistance moments ΣMc,Rd in both directions (+x, -x) και (+y, -y) and the two corresponding beam resistant moments ΣMb,Rd are added.
iv. When setbacks are present, the following additional conditions apply for each direction:
- For gradual setbacks preserving axial symmetry, the setback at any floor shall be not greater than 20 % of the previous plan dimension in the direction of the setback.
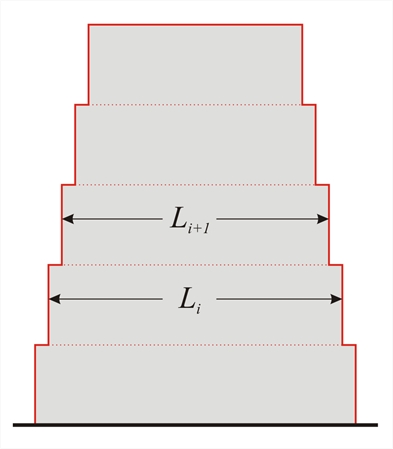 Figure 6.1.5.3-10
Figure 6.1.5.3-10 Figure 6.1.5.3-10
- If the setbacks do not preserve symmetry, in each face the sum of the setbacks at all storeys shall be not greater than 30 % of the plan dimension at the ground floor above the foundation or above the top of a rigid basement, and the individual setbacks shall be not greater than 10 % of the previous plan dimension.
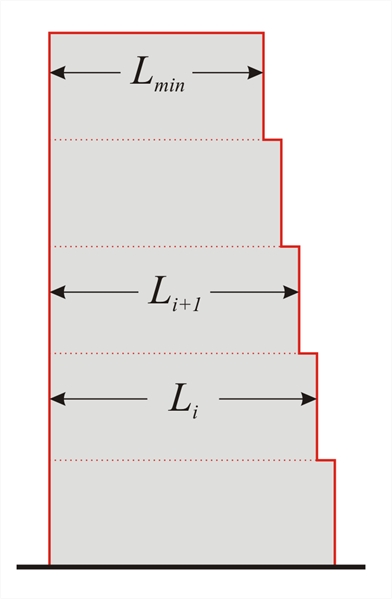 Figure 6.1.5.3-11
Figure 6.1.5.3-11 Figure 6.1.5.3-11
- For a single setback within the lower 15 % of the total height of the main structural system, the setback shall be not greater than 50 % of the previous plan dimension. In this case the structure of the base zone within the vertically projected perimeter of the upper storeys should be designed to resist at least 75% of the horizontal shear forces that would develop in that zone in a similar building without the base enlargement.
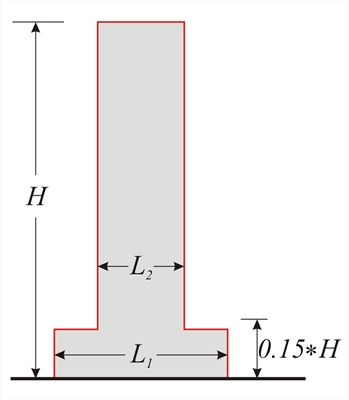 Figure 6.1.5.3-12
Figure 6.1.5.3-12 Figure 6.1.5.3-12
Ductility classes [EC8 §5.2.1]
Earthquake resistant buildings are classified in three ductility classes.
(α) DCL from the initials of Ductility Category Low
(β) DCM from the initials of Ductility Category Medium
(γ) DCH from the initials of Ductility Category High
Buildings belonging to Ductility Category Low are designed for low energy dissipation capacity and low ductility, following the provisions of EC2 that concern the dimensioning without of course accounting for the reduction of seismic forces, i.e. the behaviour factor q shallbe taken equal to 1.0. The only construction requirement concerns the use of B or C steel class [EC2, 3.2.2(3)A ].
This category is recommended for the classification of buildings in low seismicity regions.
Buildings belonging to Ductility Category Medium are designed for medium energy dissipation capacity and medium ductility, and conform to the particular design and construction rules of EC8.
Buildings belonging to Ductility Category High are designed for high energy dissipation capacity and high ductility and conform to the strictest relevant design and construction rules.
Buildings classified as frame system and brittle masonry are not allowed to belong to this class.
-
The above classification addresses to both monolithically cast-in-situ and precast buildings.
-
Concrete buildings with flat slab frames, without beams, are not fully covered by the EC8.
Basic value of the behaviour factor qo [EC8 §5.2.2.2]
| | | |
| | | | | |
Inverted pendulum system (6) | | | | |
Torsionally flexible system (7) | | | | |
Uncoupled wall system [partial case (2)] | | | | |
| | | | | |
Table 6.1.5.5-1: Basic value of the behaviour factor qo
The values of factor au/a1 may be obtained either from push over analysis or from the following table:
| | | | |
| | | | |
Frame system (1), frame-equivalent dual system (3), (4), coupled wall system (2) | | | |
Multistorey building with one-bay frame in the direction considered | | |
Rest of multistorey buildings | | |
| | | | |
Wall-equivalent dual system (4) | Two walls in the direction considered | | |
More than two walls in the direction considered | | |
Systems of large lightly reinforced walls (5) | | | |
The factor au/a1 does not need to be evaluated for inverted pendulum(6) or torsionally flexible(7) systems |
Table 6.1.5.5-2: Values of the multiplication factor au/a1
Notes on the above tables
-
For non-regular in elevation buildings the decreased values of the behaviour factor qo are obtained by the reference values multiplied by 0.80.
-
For non-regular in plan buildings the values of the multiplication factor au/a1, are obtained by the reference values according to the expression (1+au/a1)/2.
Summarizing the above results in the following table:
| | |
| | |
| | | |
| | | | | | |
| | torsionally flexible system | | | | |
| | System of large lightly reinforced walls | | | | |
| | Wall-equivalent dual system | Two walls in the direction considered | | | |
| | | | |
| | Frame or wall-equivalent dual system | | | | |
Multistorey building with one-bay frame in the direction considered | | | |
Rest of multistorey buildings | | | |
| | | Uncoupled walls in the direction considered | | | |
Coupled walls in the direction considered | | | |
regular in elevation - regular in plan: qo=aqo·au/a1 regular in elevation - non-regular in plan: qo=aqo·(1+au/a1)/2 non-regular in elevation - regular in plan: qo=0.8·aqo·au/a1 non-regular in elevation - non-regular in plan: qo=0.8·aqo· (1+au/a1)/2 |
Table 6.1.5.5-3: Basic value of the behaviour factor qo
Examples for wall-equivalent dual system (4) with more than two walls:
Regular in elevation - regular in plan :
for DCM qo=3.0 · 1.1=3.30, for DCH qo=4.5 ·1.1=4.95
Regular in elevation - non- regular in plan :
for DCM qo=3.0 · 1.05= 3.15, for DCH qo=4.5 ·1.05= 4.725
Non-regular in elevation - regular in plan :
for DCM qo=0.8 · 3.0 · 1.1=2.64, for DCH qo=0.8 · 4.5 ·1.1=3.96
Non-regular in elevation - non- regular in plan :
for DCM qo=0.8 · 3.0 · 1.05=2.52, for DCH qo=0.8 · 4.5 ·1.05=3.78
Failure mode factor kw [EC8 §5.2.2.2]
The behaviour factor is given by the expression q=kwqo≥1.5, where q ο is the basic value of the behaviour factor, presented in the previous paragraph and kw is the failure mode factor.
kw=1.0for frame systems (1), or frame-equivalent dual systems (3), while for the remaining wall systems (2), (4), (5),Kw=(1+ao)/3, where ao is the aspect ratio of the walls equal to ao=Σhw,i/Σlw,i. In any casekw should satisfy the relation 0.50≤kw≤1.0.
The failure mode factor kw is ≤1.0 provided that ao≤2.0, meaning walls of averagelength lw>hw/2, i.e. in a one-storey building of height hw=3.0 m for walls of lengthlw>3.0/2=1.50 m, in a two-storey building ofhw=2·3.0=6.0 m for walls of lw>6.0/2=3.0 m and, respectively, in a similar four-storey building for walls of lw>6.0 m and for aten-storey building for walls of lw>15 m. For common multistorey buildings without large lightly reinforced walls, applies kw=1.0.
A few brief results, based on the previous paragraphs, are presented here:
-
For common buildings, the behaviour factor q is equal to the basic behaviour factor qo, i.e. q=qo.
-
For DCM q varies between 1.50 and 3.90 while, for DCH q varies between 1.60 and 5.85.
-
In inverted pendulum systems (6) q is independent of the regularity in plan. For DCM q, is also independent of the regularity in elevation and is equal to 1.50, while for DCH q is equal to 1.60 or 2.0.
-
In torsionally flexible systems (7) q is independent of the regularity in plan. For DCM q is 1.60 or 2.0 while for DCH is 2.40 or 3.0.
-
In wall-equivalent dual systems (4), for DCM q varies between 2.40 and 3.30 while for DCH q varies between 3.60 and 4.95.
-
-
In frame (1) or frame-equivalent dual systems (3), the maximum values of q apply. For DCM q varies between 2.88 and 3.90 while for DCH q varies between 4.32 and 5.85. The seismic design of masonry frame systems is not allowed, in general.
-
The minimum value of the behaviour factor, q=1.50, may be selected for every simple or complex building, without structural type classification or regularity criteria compliance. Such selection beyond the safety reasons also covers the case of radical structural change due to renovation, change of use or other reason, during the building lifetime.
-
The assumption of q=1.0 combined with the classification, regarding the construction rules, to DCM or even better to DCH, isdefinitely a good choice for the seismic design of buildings. Certainly, if the building is designed appropriately, achieving value of q higher than e.g. 3.50, high standards of safety would be reached.