|
« Structural model
Effective width of flanges [EC2 A§5.3.2.1] »
|
Effective span of beams and slabs [EC2 A§5.3.2.2] 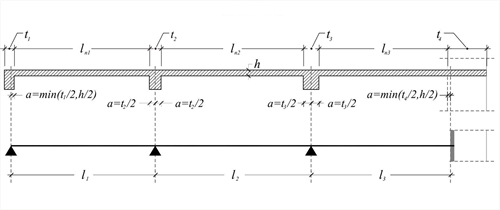 Figure 3.1.1
Figure 3.1.1 Figure 3.1.1 Τhe effective span leff of a slab or beam is calculated by the expression: l eff =l n +a left +a right where ln is the clear distance between the lateral faces of the supports, and a=min(t/2,h/2) is the width of the support. -
At the end support of the first slab, the width is considered to be a=t1/2=125 mm which is acceptable as in favor of the safety. -
The width of beam-to-column supports, is taken into account more efficiently, when the analysis uses rigid bodies (see §3.1.3).
Consider continuous slabs with thickness: h=150 mm, width of supports: t1=250 mm, t2=300 mm, t3=400 mm, t4 =1000 mm, clear spans: ln1=3700 mm, ln2=4000 mm, ln3=4000 mm. The effective spans of slabs are equal to: l1=3700+min(250/2,150/2)+300/2=3925 mm l2=4000+300/2+400/2=4350 mm l3=4000+400/2+min(1000/2,150/2)=4275 mm. Example 3.1.1-2 Consider continuous beams with height: h=500 mm, width of supports: t1=250 mm, t2=300 mm, t3=400 mm, t4=1000 mm, clear spans: ln1=3700 mm, ln2=4000 mm, ln3=4000 mm. The effective spans of beams are equal to: l1=3700+min(250/2,500/2)+300/2=3975 mm l2=4000+300/2+400/2=4350 mm l3=4000+400/2+min(1000/2,500/2)=4450 mm.
|
« Structural model
Effective width of flanges [EC2 A§5.3.2.1] »
|

|