Slab bar AB of length L, moment of inertia I, elasticity modulus E, is subjected to uniform load p. Given shear force VA,R(at left support) and bending moment MA, calculate equation of elastic line due to bending and maximum deflection. 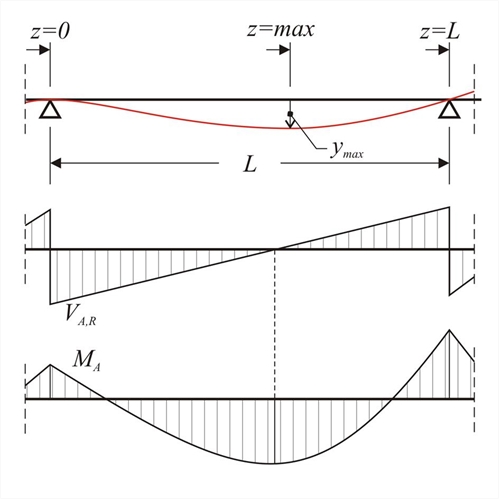 Figure 4.5.2-1: General case of bending of bar (slab or beam)
Figure 4.5.2-1: General case of bending of bar (slab or beam) Figure 4.5.2-1: General case of bending of bar (slab or beam) Considering coordinate z origin at the left end:
of the elastic line is solved in two steps:
Hence, the equation of the elastic line tangents is:
Hence, the equation of the elastic line is :
Thus, the equations of the elastic line tangents (1) and deflections (2) are determined. The maximum deflection is at the location where the first derivative of the elastic line equation is zero, i.e. at the point z where φ(z) =0.
The real positive root of the cubic equation (3) gives the desired point zmax, which replaced in equation (2) yields the maximum deflection ymax.
Example: Deflection of first slab (example of §4.3.1): For L=4.5 m, p=16.5 kN/m, VA,R=32.1 kN and MA=0.0, expression (3) yields:
(4) > (16.5/6)·z3-(32.1/2)·z2-0+45.7=0 > 2.75z3-16.05z2+45.7=0 > z max=2.112 m (2) > For slab thickness h=180 mm and modulus of elasticity for concrete E=32.80 GPa: I=(b·h3)/12=(1.0x0.183)/12=486x10-6 m4 E·I=32.8x109N/m2x486x10-6m4=15.9408x106 N·m2, therefore,
Example: Deflection of second slab (example of §4.3.1): For L=4.0 m, p=9.75 kN/m, VA,R=21.7 kN and MA=-22.6 kNm, expression (3) yields:
(4) > (9.75/6)·z3-(21.7/2)·z2+22.6z-13.333=0 > 1.625z3-10.85z2+22.6z-13.333=0 > zmax=0.993m
For slab thickness h=140 mm and modulus of elasticity for concrete E=32.80 GPa: I=(b·h3)/12=1.0x0.143/12=228.7x10-6 m4 E·I=32.8x109N/m2x228.7x10-6m4=7.5014x106 N·m, therefore,
Example: Deflection of third slab (example of §4.3.1): For L=4.0 m, p=9.75 kN/m, VA,R=23.0 kN and MA=-13.9 kNm, expression (3) yields: C1=(-9.75x4.03/24+23.0x4.02/6-13.9x4.0/2) kN·m2 =7.533 kN·m2 (4) > (9.75/6)·z3-(23.0/2)·z2+13.9z+7.533=0 a 1.625z3-11.50z2+13.9z+7.533=0 a zmax=2.181m
For slab thickness h=140 mm and modulus of elasticity for concrete E=32.80 GPa: I=(b·h3)/12=1.0x0.143/12=228.7x10-6 m4 E·I=32.8x109N/m2x228.7x10-6m4=7.5014x106 N·m2, therefore,
The elastic line of the continuous slab given by expressions (1.2), (2.2), (3.2) is illustrated in the following figure: .jpg?bhow=0&w=500&h=500&Str=0) Figure 4.5.2-2: The elastic line of the three slabs (from the equations)
Figure 4.5.2-2: The elastic line of the three slabs (from the equations) Figure 4.5.2-2: The elastic line of the three slabs (from the equations)
Project <B_451> (pi-FES) produces identical deflections:  Figure 4.5.2-3: Front view of the elastic line (from pi-FES with active module\SLABS)
Figure 4.5.2-3: Front view of the elastic line (from pi-FES with active module\SLABS) Figure 4.5.2-3: Front view of the elastic line (from pi-FES with active module\SLABS)
|