The fixity degree varies from fixed to pinned. When a weak column (e.g. cross-section 300/300) is connected to strong beams (e.g. concrete beams with height 800 mm) the connection could be considered as fixed. On the contrary, when the column top is connected to a plain slab and the column base is connected to weak footing in soft soil without foundation beams, the connections could be idealised as pinned.
H = K· δ
The term K denotes the stiffness of the one-end-fixed column.
kv ais the correction factor of the bending stiffness of the one-end-fixed column due to shearing. Always kva <1.0. It can be ignored for ordinary columns (i.e. it may be assumed that kva=1.0)while for walls kva should be taken into account.
Consider an one-end-fixed column with cross-section 400m m /400 mm , height h =3.0 m , elasticity modulus E =32.8 GP , bearing a concentrated mass of m =80 t at the top. The seismic acceleration design factor at top is a / g =0.10.
Calculate the stress resultants and relative displacement at top.
W =80 · 1000 kg · 10 m / sec 2 =800 kN , H =0.10·800=80 kN , V = H =80 kN
M 1 =0 and Μ 2 =- H · h =-80·3.0=-240 kNm
I =0.40·0.403/12=21.33·10-4 m 4
Without shear effect, K=3 · EI / h 3 =3 · 32.8 · 109 · Ν /m2 · 21.33 · 10-4m4/(3.03 · m3)=7.77·106 N / m .
With shear effect, for G=0.5E, kz=5/6 (rectangular cross-section) and A=b · d: This expression is independent of the cross-sectional width and applies to all one-end-fixed rectangular columns.
For this particular column
Without shear effect, δ =H/K=80 · 103N/(7.77 · 106N/ m ) =10.30 mm .
With shear effect, δ =H/K=80 · 103N/(7.69 · 106N/ m ) =10.40 mm , i.e. the displacement is 1% higher than the respective value without shear effect.
Consider the data and questions of the previous example for a wall with cross-section 2000/300.
W =80 · 1000 kg · 10 m / sec 2 =800 kN , H =0.10·800=80 kN , V = H =80 kN
M 1 =- Μ 2 =- H · h /2=-80·3.0/2=120 kNm
I =0.30·2.003/12=0.20 m 4
Without shear effect, K=3 · EI / h 3 =3 · 32.8 · 109 · Ν /m2 · 0.20m4/(3.03 · m3)=728.89·106 N / m .
For this particular column
Therefore without shear effect, δ =H/K=80 · 103N/(728.89 · 106N/ m )=0.110 mm .
With shear effect, δ =H/K=80 · 103N/(575.10 · 106N/ m ) =0.139 mm , i.e. the displacement is 26% higher than the respective value without shear effect.
In the case of a column pinned at both ends, the equivalent member is not subjected to bending thus carrying neither bending moments nor shear forces. Indicatively, the case of a pin-ended column could be met at a storey without beams, at the roof and at the floor.
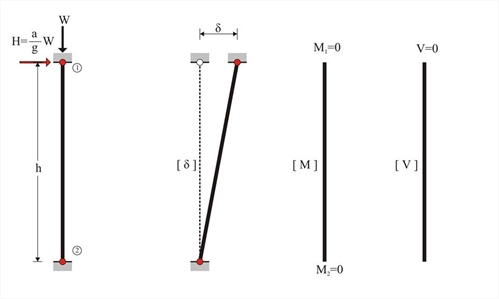 Figure 5.1.2-2
Figure 5.1.2-2 Figure 5.1.2-2
The three previous columns, i.e. having either both ends fixed or one end fixed or both ends pinned, are considered to compose a one-storey frame. All columns have the same material and cross-section 400/400 therefore the same E·I. The same mass at the top and therefore the same seismic load H is also applied to them. Due to the presence of the slab, the axial deformation of the frame crossbar may be practically ignored. In case of seismic action, each column top would be forced to develop identical displacement δ regardless of its stiffness.
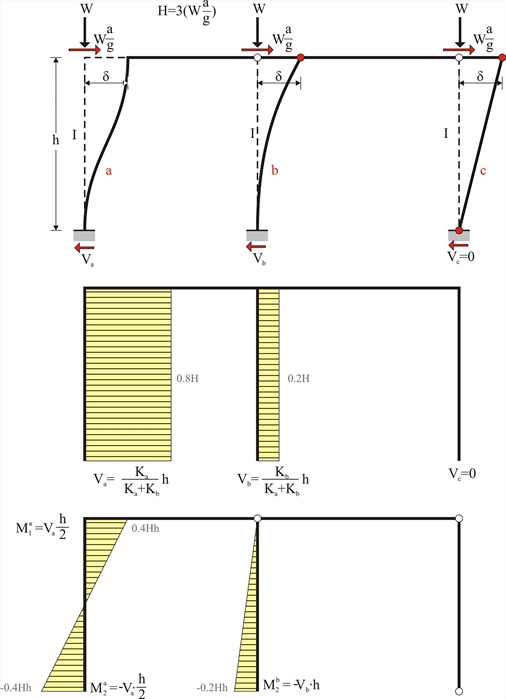 Figure 5.1.2-3: 80% of the seismic force is carried by the fixed-ended column
Figure 5.1.2-3: 80% of the seismic force is carried by the fixed-ended column Figure 5.1.2-3: 80% of the seismic force is carried by the fixed-ended column