The residential building of the sketch includes a basement of area 12x18 m2 and height 3 m, a ground floor and four storeys of identical dimensions and a top floor of area 4x6 m2 and height 2.5 m. The masses at levels 0, 1, 2, 3, 4 are equal to MG=220 t and MQ=44 t, at level 5 to MG=180 t and MQ=44 t, while at the top level to MG=20 t and MQ =4 t. The building is situated in the seismic area Z1 and the distribution of seismic accelerations is triangular. The design seismic acceleration The calculation of the seismic and wind forces as well as a comparison between them is asked. .jpg?bhow=0&w=500&h=500&Str=0) Figure 2.5-1: The geometrical and loading model of the building's wind and earthquake actions
Figure 2.5-1: The geometrical and loading model of the building's wind and earthquake actions Figure 2.5-1: The geometrical and loading model of the building's wind and earthquake actions Mi [t] : masses, w [kN/m2]: wind loads, ai[m/sec2 ]: seismic accelerations Since the building is residential ψ2=0.30 and consequently during an earthquake the dynamic masses are evaluated asM=MG+0.30·MQ. Thus, the dynamic masses at levels 0, 1, 2, 3 and 4 are equal to M G+0.30Q,i=0-4=220+0.30x44=233 t, at level 5 is equal to MG+0.30Q,5=180+0.30x44=193 t, while at the top level is equal MG+0.30Q,6=20+0.30x4=21 t. 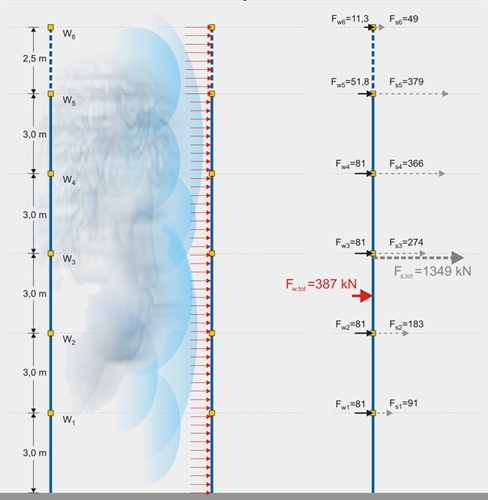 Figure 2.5-2: Wind forces Fw are less significant comparing to earthquake forces Fs.
Figure 2.5-2: Wind forces Fw are less significant comparing to earthquake forces Fs. Figure 2.5-2: Wind forces Fw are less significant comparing to earthquake forces Fs. W [kN]:gravity loads Fw [kN]: windforces Fs [kN]: seismic forces Assessment of seismic forces The total mass of the building during earthquake is M=4x233+193+21=1146 t, while the CM (mass center) is located at distance zοfrom the ground floor basis:
The design acceleration at the CM is 0.12g. Therefore acceleration at the 1st level is equal to a1 =(3.0/9.0)x0.12g=0.04g. Respectively, at the rest levels: a 2 =0.08g , a3=0.12g, a4=0.16g, a5=0.20g and a6 =0.24g. The seismic force imposed on level 'i' is: F s,1 =233t · (0.04x9.81)m/sec 2 =91 kN F s,2 =233t · (0.08x9.81)m/sec 2 =183 kN F s,3 =233t · (0.12x9.81)m/sec 2 =274 kN F s,4 =233t · (0.16x9.81)m/sec 2 =366 kN F s,5 =193t · (0.20x9.81)m/sec 2 =379 kN F s,6 =21t · (0.24x9.81)m/sec 2 =49 kN The total seismic force (or the total seismic base shear force) Fs,tot is equal to the sum seismic forces at different levels and its center of application is located at about 2/3 of the building height. F s,tot =1146t · (0.12x9.81)m/sec 2 =1349 kN Assessment of wind forces For maximum wind load w=1.50 kN/m2, the corresponding force towards the most unfavourable vertical direction of the 18.0 m on each storey is Fw=18.0m·3.0m·1.50kN/m2=81 kN,
while on the top floor is Fw=6.0m·2.5m·1.50kN/m2=23 kN.
The wind load on each storey is equally shared between the two levels defining it. Therefore, 6th level: Fw,6=23/2=12 kN 5th level: Fw,5=23/2+81/2=52 kN Rest levels: Fw,i=0-4=81/2+81/2=81 kN The total wind force is Nw,tot=12+52+4x81=388 kN and its point of application is located at about 1/2 of the building height. Comparison of wind and seismic forces
|