Exercise 4.9.2|www.BuildingHow.com

VOLUME A
The art of construction and detailing
Introduction
The structural frame
- Introduction
- Structural frame elements
  - Columns
  - Beams
  - Slabs
  - Staircases
  - Foundation
- STRUCTURAL FRAME LOADING
- BEHAVIOR OF THE STRUCTURAL FRAME
  - The behavior and reinforcement of a slab
  - Behavior and reinforcement of beams and columns
Construction methods
- The materials
- The moulds
- Thermal insulation of structural elements
- Concrete
- The steel
- Reinforcement specifications of antiseismic design
- Industrial stirrups - stirrup cages
- Standardized cross-sections of reinforced concrete elements
Reinforcement
- Columns
- Shear walls
- Composite elements
- Beams
- Slabs
- Staircases
- Foundation
Quantity surveying
- Estimation of the concrete’s quantity
- Estimation of the formworks’ quantity
- Estimation of the spacers’ quantity
- Estimation of the reinforcements' quantity
- Total estimation of the materials’ quantities
- Optimization of the reinforcement schedule
- Estimation of the structural frame’s cost
- Electronic exchange of designs - bids - orders
Detailing drawings
- General
- The drawings’ title block
- Carpenter’s drawings
- Steel fixer’s drawings
Tables
- Table 1
- Table 2
- Table 3
Drawings
- Carpenter’s drawings
- Steel fixer’s drawings
Model (exemplary) construction

« Exercise 4.9.1 Exercise 4.9.3 »

Exercise 4.9.2

Given : Covering load g_e=1.5 kN/m², live load q=2.0 kN/m², concrete quality C40/50 (E=35.2 GPa).

Question : Perform static analysis to calculate bending moments, shear forces, reaction forces, deflections and equivalent uniform loadings of slabs transferred onto beams.

Figure 4.9.2-1: Project <B_49-2>

Solution:

Self-weight	g _o =0.15m25.0kN/m³=	3.75 kN/m²
Covering load	g _e =	1.50 kN/m²
Total dead load	g₁=g₂=	5.25 kN/m²
Total live load	q₁=q₂=	2.00 kN/m²
Design load	p₁=p₂=γ_gx5.25+γ_qx2.0= =1.35x5.25+1.50x2.0=	10.09 kN/m²

Marcus method:

Coordinate system of the slabs is considered rotated by 90^ο.

Figure 4.9.2-2

s1 : ε=l_y'/l_x'=1.20. From table b5.2: k_x=0.453, k_y=0.547,

v_x=0.738, v_y=0.631, a_m=0.0523, ρ_xr=ρ_yr=0.439, ρ_yerm=0.761, υ_xr=0.220, υ_yr=0.246, υ_yerm=0.427 →

p_x=k_x p=0.453x10.09=4.57, p_y=k_y p=0.547x10.09=5.52 kN/m

M_x=ν_x·p_x · l_x²/8=0.738x4.57x5.0²/8=10.54 kNm

M_y=ν_y·p_y · l_y²/14.22=0.631x5.52x6.0²/14.22=8.82 kNm

M_yerm=-p_y·l_y²/8=-5.52x6.0²/8=-24.84 kNm

f_m=0.0523x10.09x10³N/m²x5.0⁴m⁴/(35.20x10⁹N/m²x1.0mx0.15³m ³)= =2776x10^-6m=2.78 mm

V_xr=V_yr=ρ_xr·p·l_x=0.439x10.09x5.0=22.15 kN

V_yerm=ρ_yerm·p·l_x=0.761x10.09x5.0=38.39 kN

p_xr=υ_xr·p·l_x=0.220x10.09x5.0=11.10 kN/m

p_yr=υ_yr·p·l_x=0.246x10.09x5.0=12.41 kN/m

p_yerm=υ_yerm·p·l_x=0.427x10.09x5.0=21.54 kN/m

Figure 4.9.2-3

s2 : ε=l_y/l_x=4.0/5.0=0.80. From table b5.2: k_x=0.141, k_y=0.859, v_x=0.817, v_y=0.742, a_m=0.0180, ρ_xr=ρ_yr=0.293, ρ_yerm=0.507, υ_xr=0.146, υ_yr=0.207, υ_yerm=0.359 a

p_x=k_x·p=0.141x10.09=1.42 kN/m, p_y=k_y · p=0.859x10.09=8.67 kN/m M_x=ν_x·p_x·l_x²/8=0.817x1.42x5.0²/8=3.63 kNm

M_y=ν_y·p_y · l_y²/14.22=0.742x8.67x4.0²/14.22=7.24 kNm

M_yerm=-p_y·l_y²/8=-8.67x4.0²/8=-17.34 kNm

f_m=0.0180x10.09x10³N/m²x5.0⁴m⁴/(35.20x10⁹N/m²x1.0mx0.15³m ³)=955x10^-6m=0.96 mm

V_xr=V_yr=ρ_xr·p·l_x=0.293x10.09x5.0=14.78 kN

V_yerm=ρ_yerm·p·l_x=0.507x10.09x5.0=25.58 kN

p_xr=υ_xr·p·l_x=0.146x10.09x5.0=7.37 kN/m

p_yr=υ_yr·p·l_x=0.207x10.09x5.0=10.44 kN/m

p_yerm=υ_yerm·p·l_x=0.359x10.09x5.0=18.11 kN/m

Support s1-s2: M_1-2=-(24.84+17.34)/2=-21.09 kNm

Results are transferred to the initial coordinate system producing the following stress resultants

M_x,1-2=-21.09, M_x,1=8.82, M_y,1=10.54, M_x,2=7.24, M_y,2=3.63 [kNm]

V_xr,1=22.15, V_xerm,1=38.39, V_yr,1=22.15, V_xerm,2=25.58, V_xr,2=14.78, V_yr,2=14.78 [kN]

equivalent uniform support reactions:

p_xr,1=12.41, p_xerm,1=21.54, p_yr,1=11.10, p_xerm,2=18.11, p_xr,2=10.44, p_yr,2=7.37 [kN/m]

and loads on beams:

b1 and b3: p=12.41, b5: p=11.10, b6: p=21.54+18.11=39.65, b2 and b4: p=7.37, b7: p=10.44 [kN/m]

Finite element method:

In project < B_49-2> the following results are obtained by activating module "SLABS" in pi-FES: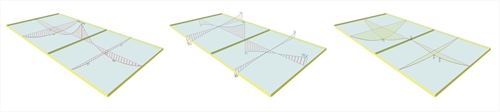

Figure 4.9.2-4: Results summary from "Slab Results" module in pi-FES Figure 4.9.2-4: Results summary from "Slab Results" module in pi-FES
M_x,1-2=-20.0 kNm M_x,1=8.5 kNm, M_y,1=10.2 kNm M_x,2=7.1 kNm, M_y,2=2.7 kNm	V_xr,1=16.8 kN, V_yr,1=16.7 kN V_yerm,1=28.9 kN V_xr,2=13.1 kN, V_yr,2=10.2 kN V_yerm,2=27.0 kN	y₁=-2.91 mm y₂=-0.85 mm

Figure 4.9.2-5: Analytical results from ‘FEM Results’ Figure 4.9.2-5: Analytical results from ‘FEM Results’
Bending moment distribution M₁₁	Shear force distribution V₁₁	Deflections

« Exercise 4.9.1 Exercise 4.9.3 »