|
« The frame function in regions of columns
Torsional stiffness of beams »
|
Vertical deformation of beams 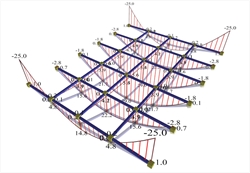 Figure 3.3.6.2-1: Bending moments of joists supported on beams 300/1000
Figure 3.3.6.2-1: Bending moments of joists supported on beams 300/1000 Figure 3.3.6.2-1: Bending moments of joists supported on beams 300/1000 | 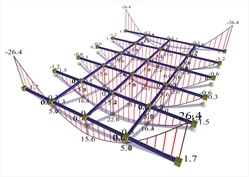 Figure 3.3.6.2-2: Bending moments of joists supported on beams 300/500
Figure 3.3.6.2-2: Bending moments of joists supported on beams 300/500 Figure 3.3.6.2-2: Bending moments of joists supported on beams 300/500 |  Figure 3.3.6.2-3: Bending moments of joists supported on beams 300/300
Figure 3.3.6.2-3: Bending moments of joists supported on beams 300/300 Figure 3.3.6.2-3: Bending moments of joists supported on beams 300/300 |
The traditional static analysis considers beams as practically undeformed. Nowadays, with the accurate analysis using finite elements, it is possible to form structures of remarkably higher stiffness of beams than slabs. In order to study the effect of vertical deformation of support beams, we examined parametrically their height (1000, 500, 300 mm). In both models, the effect of vertical deformation of beams to the deformation of the slab is insignificant for beams with cross-section 300/1000 (deformations of beams practically zero), moderate for 300/500 (considerably smaller with respect to those of the slab) and significant for 300/300. In the two-dimensional finite element method, the secondary bending moments are always significant, while the moments in the main direction remain relatively constant. In conclusion, the assumptions of beam bar elements as frame elements and of two-dimensional elements as slab elements are considered to be both logical and successful. This success is greater the stronger the beams cross-section (mainly their depth), the smaller their span, and also the smaller the thickness of the slabs is. 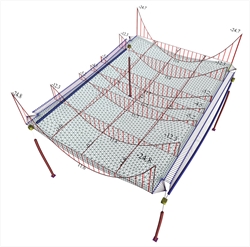 Figure 3.3.6.2-4: Bending moments of joists supported on beams 300/1000
Figure 3.3.6.2-4: Bending moments of joists supported on beams 300/1000 Figure 3.3.6.2-4: Bending moments of joists supported on beams 300/1000 | 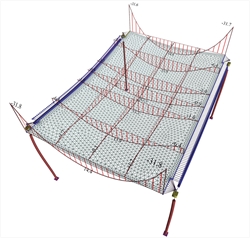 Figure 3.3.6.2-5: Bending moments of joists supported on beams 300/500
Figure 3.3.6.2-5: Bending moments of joists supported on beams 300/500 Figure 3.3.6.2-5: Bending moments of joists supported on beams 300/500 |  Figure 3.3.6.2-6: Bending moments of joists supported on beams 300/300
Figure 3.3.6.2-6: Bending moments of joists supported on beams 300/300 Figure 3.3.6.2-6: Bending moments of joists supported on beams 300/300 |
Once the structure's formwork is demolded, significant moments develop at the slab-to-beam connections, both relieving slab bending and aggravating beam torsion. However, due to creep of concrete, the torsional deformation of the beam increases gradually causing the reduction of bending and torsional moments on the beam, while the support tends to develop into a hinge, while maintaining a small degree of fixity. That is why EC2 in §6.3.1(2) states that '… in these cases it will normally be unnecessary to consider torsion at the ultimate limit state'.
|
« The frame function in regions of columns
Torsional stiffness of beams »
|

|