|
« Work methodology
One-storey space frame with rectangular columns in parallel arrangement »
|
Assessment of building torsional behaviour The degree of the torsional stiffness of a diaphragmatic floor is determined by the relation between the equivalent mass inertial ring (CM, ls) and the torsional stiffness ellipse (CT, rx, ry). The optimal location of the two curves is where the torsional stiffness ellipse encloses the mass inertial ring. 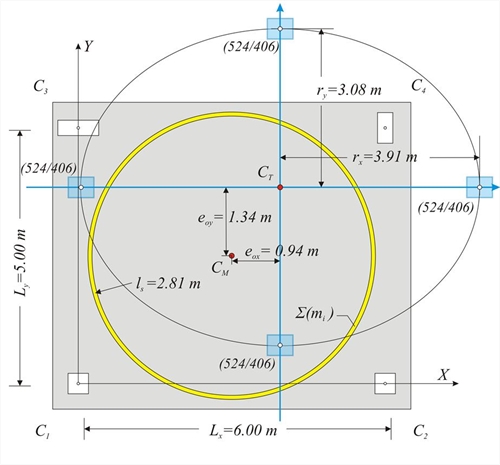 Figure 5.4.4: Equivalent mass inertial ring (CM, ls) and torsional stiffness ellipse (CT, rx, ry
Figure 5.4.4: Equivalent mass inertial ring (CM, ls) and torsional stiffness ellipse (CT, rx, ry Figure 5.4.4: Equivalent mass inertial ring (CM, ls) and torsional stiffness ellipse (CT, rx, ry A building is classified as torsionally flexible [EC8 §5.2.2.1] if either rx<ls or ry<ls is satisfied in at least one diaphragm storey level. In this example both conditions are satisfied. For a building to be categorized as being regular in plan, the two structural eccentricities eox, eoy at eachlevel shall satisfy both conditions eox≤0.30rx & eoy≤0.30ry [EC8 §4.2.3.2]. In this particular example the first condition is satisfied eox=0.94 m ≤ 0.30rx (=0.30×3.91=1.173 m), whereas the second one is not eox=1.34 m ≤ 0.30rx (=0.30×3.08=0.924 m). Therefore the building that comprises that specific floor diaphragm is not regular in plan. Simplified seismic analysis may be performed, provided that the following conditions are met for each x, y direction: r y 2 > ls2 + eoy2 [EC8 §4.3.3.1(8) d)]. In this example the first condition is satisfied 3.912(=15.3)>2.812+0.942(=7.9+0.9=8.8) , whereas the second one is not 3.082(=9.5)<2.812+1.342(=7.9+1.8=9.7) . We therefore conclude that the simplified seismic analysis may not be performed at the building including this particular floor diaphragm.
In case the slab loads would be uniformly distributed (§5.3.2), then ls=2.25 m and the last requirement would be met. This theory applies to any case of a multi-storey building floor. The only difference is the complicated calculation method for the stiffnesses (practically requiring space frame analysis). The self-torsional stiffness factors listed in the following table are verified by the expression of §5.4.3.4. | d/b | 1 | 1.5 | 2.0 | 3.0 | 4.0 | 6.0 | 10 | ∞ | | n | 0.1415 | 0.1964 | 0.2292 | 0.2636 | 0.2810 | 0.2985 | 0.3124 | 0.3333 |
|
« Work methodology
One-storey space frame with rectangular columns in parallel arrangement »
|

|