|
OF MULTISTOREY SPACE FRAMES GENERAL CASE The assessment of the behaviour of one-storey plane frames under horizontal seismic forces was presented in paragraph 5.1, where the structural unit examined was the column (or wall). In appendix Β, the crossbar was used to assess the behaviour of the multistorey plane frame. In this chapter, the composition of space frames, through beams and slabs, is considered. The diaphragm is the structural unit for the assessment of coupled space frames. Studying paragraph 5.4 and Appendices B and C is recommended in order to better understand this chapter.  Figure D.1-1: The structural frame with 6 levels, project
Figure D.1-1: The structural frame with 6 levels, project Figure D.1-1: The structural frame with 6 levels, project
A diaphragm is the horizontal part of the floor consisting of slabs, connecting beams and columns. A floor may comprise more than one diaphragm, as shown in the example building of the present paragraph.  Figure D.1-2: The space frame structural model with bars of columns and beams and diaphragms
Figure D.1-2: The space frame structural model with bars of columns and beams and diaphragms Figure D.1-2: The space frame structural model with bars of columns and beams and diaphragms
The most characteristic point of the diaphragm is the centre of stiffness, described in paragraphs 3.1.4, 5.4.3.4 and C.5. The centre of stiffness CT of a specific floor diaphragm is defined as the point about which the diaphragm rotates, under horizontal seismic force H. The CT point depends only on the geometry of the floor and is independent of the loadings, meaning that regardless the magnitude of the force, which may become equal to 2H, or 3H, or any other value, the centre of stiffness will remain the same. Of course, it depends on the geometry of the overlying and the underlying floors. Principal axis system of diaphragm is defined as the orthogonal axis system xCTy, in which when a horizontal seismic force H is applied on CT, along axis x (or y), it results in translating CT only along axis x (or y respectively). The angle a of the principal system, as to the initial system X0Y, is called principal angle of the diaphragm. The above diaphragm data as well as the torsional stiffness Kθ and torsional ellipse stiffness ellipse ( CT, rx, ry), should be calculated in a general way. The method to be used should deal with more than one diaphragm per floor. Moreover, the general solution should account for the influence of non-diaphragmatic frames as well as the uneven level foundation. All possible special cases met in practice are included in the example presented in this paragraph, except for foundations, just for simplification reasons. Full scale analysis (including the foundation), can be performed by the engineer using the related software. 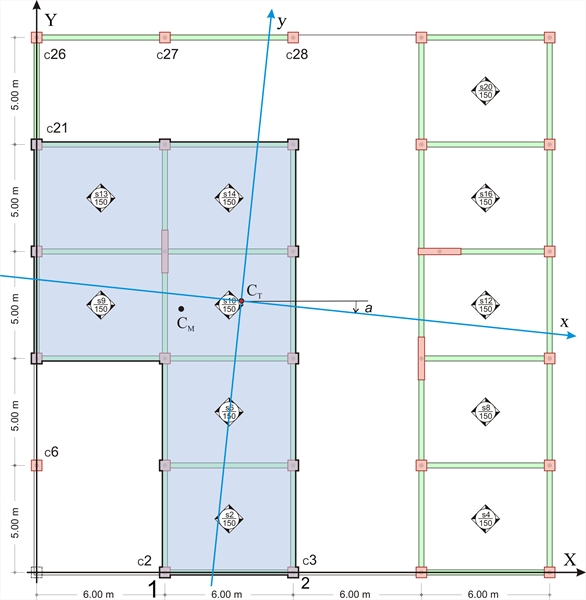 Figure D.1-3: Floor plan of 5th level and diaphragm on the left examined next.The cross-sections of columns, walls and beams are 500/500, 2000/300 and 300/500 respectively.
Figure D.1-3: Floor plan of 5th level and diaphragm on the left examined next.The cross-sections of columns, walls and beams are 500/500, 2000/300 and 300/500 respectively. Figure D.1-3: Floor plan of 5th level and diaphragm on the left examined next.The cross-sections of columns, walls and beams are 500/500, 2000/300 and 300/500 respectively.
The behaviour of diaphragm on the left at the 5th level, analysed next is directly affected by the L-type frame C21-C 26-C27-C28 connected to it and indirectly by column C6 and the diaphragm on the right, through the frames of other floors. A general method for the calculation of the diaphragm data is presented next. This method creates a condition allowing the diaphragm only to rotate about the centre of stiffness CT, which remains stationary with respect to the ground. The method comprises four steps, the first three of which include a space frame analysis.
D.2 General method for the calculation of the diaphragm i data Step 1 : Analysis under force HΧ and concentrated moment MCM,X applied at the centre of mass of diaphragm i. .jpg?bhow=0&w=600&h=600&Str=0) Figure D.2-1: Loading: Force HX=100 and moment MCM,X on centre of mass CM of diaphragm iResults: total displacements of structure and displacements of diaphragm i
Figure D.2-1: Loading: Force HX=100 and moment MCM,X on centre of mass CM of diaphragm iResults: total displacements of structure and displacements of diaphragm i Figure D.2-1: Loading: Force HX=100 and moment MCM,X on centre of mass CM of diaphragm iResults: total displacements of structure and displacements of diaphragm i
The two displacements δXX1, δXY1 of point 1 of diaphragm i and its angle θ XZ are required. Any value may be given to force HΧ, as long as it is the same for the analyses of the three first steps. In this example, HΧ is given equal to 100 kN. The application point of force H is irrelevant, but for higher accuracy in calculations, the force is assumed applied at an arbitrary eccentricity cy, e.g. 2.0 m, in relation to the centre of mass, in order to produce a significant rotation of the diaphragm and thus achieve a higher accuracy in the calculations. That eccentricity isessential, especially in cases where the centre of stiffness is close or coincides with the centre of mass. Therefore, in addition to force H Χ, momentMCM,x=100kN·2.00m= 200 kNm is also applied at CM. The magnitude of force H needs to be important enough to result in significant diaphragm translations that can be distinguished from the translations due to moment. The application of the sole moment in the absence of force H results in rotation, but also in translations, which cannot be calculated since the centre of stiffness is still unknown. Point 1 corresponds to column Κ2 joint, but could be any point of the diaphragm. .jpg?bhow=0&w=600&h=600&Str=0) Figure D.2-2: The diaphragm displacements in plan, due to 2 parallel translations δXXo, δXYo and one rotation Θxz
Figure D.2-2: The diaphragm displacements in plan, due to 2 parallel translations δXXo, δXYo and one rotation Θxz Figure D.2-2: The diaphragm displacements in plan, due to 2 parallel translations δXXo, δXYo and one rotation Θxz
The only results needed from this analysis are the translations of point 1 δXX1=2.681 mm, δ XY1=-0.231 mm and the angle θXZ=4.5613·10-5 of the diaphragm. The displacements of point 2 will be used only to verify the generality of the method. All displacements are absolute with respect to the ground. Step 2 : Analysis under force HΧ applied at the centre of mass of diaphragm i with rotational restraint. .jpg?bhow=0&w=600&h=600&Str=0) Figure D.2-3: Loading: HX=100 on diaphragm i with rotational restraintResults: the total displacements of structure and the two parallel translations of diaphragm
Figure D.2-3: Loading: HX=100 on diaphragm i with rotational restraintResults: the total displacements of structure and the two parallel translations of diaphragm Figure D.2-3: Loading: HX=100 on diaphragm i with rotational restraintResults: the total displacements of structure and the two parallel translations of diaphragm
Figure D.2-3: Loading: HX=100 on diaphragm i with rotational restraint Results: the total displacements of structure and the two parallel translations of diaphragm The two translations of point 1 δXXo, δXYo, are only required, being identical for any point of the diaphragm i, thus also for CT, since the angle of rotation of the diaphragm is zero.
.jpg?bhow=0&w=600&h=600&Str=0) Figure D.2-4: The 2 parallel translations of the diaphragm δXXo, δXYo, in plan.All diaphragm points, thus also CT, have identical displacements.Diaphragm is restrained against rotation, therefore θXZ=0.
Figure D.2-4: The 2 parallel translations of the diaphragm δXXo, δXYo, in plan.All diaphragm points, thus also CT, have identical displacements.Diaphragm is restrained against rotation, therefore θXZ=0. Figure D.2-4: The 2 parallel translations of the diaphragm δXXo, δXYo, in plan.All diaphragm points, thus also CT, have identical displacements.Diaphragm is restrained against rotation, therefore θXZ=0.
All diaphragm points, thus also CT, have identical displacements. Diaphragm is restrained against rotation, therefore θXZ=0. Due to zero rotation of diaphragm i, point 1 has only two parallel translations, δXXo=2.103 mm and δ XYo=-0.047mm, being identical for all diaphragm points, thus also for CT. In other diaphragms located in the same, upper or lower level, small, yet measurable rotations exist, thus every point on them has different displacements.
Step 3 : Analysis under force HΥ applied at the centre of mass of diaphragm i with rotational restraint .jpg?bhow=0&w=600&h=600&Str=0) Figure D.2-5: Loading: HY=100 on diaphragm i with rotational restraint Results: the total displacements of structure and the two parallel translations of diaphragm
Figure D.2-5: Loading: HY=100 on diaphragm i with rotational restraint Results: the total displacements of structure and the two parallel translations of diaphragm Figure D.2-5: Loading: HY=100 on diaphragm i with rotational restraint Results: the total displacements of structure and the two parallel translations of diaphragm
The two translations of point 1 δXXo, δXYo, are only required, being identical for any point of the diaphragm i, thus also for CT, provided that the angle of rotation of the diaphragm is zero.
.jpg?bhow=0&w=600&h=600&Str=0) Figure D.2-6: The 2 parallel diaphragm translations δXXo, δXYo, in plan.All diaphragm points, thus also CT, have identical displacements.Diaphragm is restrained against rotation, therefore θXZ=0.
Figure D.2-6: The 2 parallel diaphragm translations δXXo, δXYo, in plan.All diaphragm points, thus also CT, have identical displacements.Diaphragm is restrained against rotation, therefore θXZ=0. Figure D.2-6: The 2 parallel diaphragm translations δXXo, δXYo, in plan.All diaphragm points, thus also CT, have identical displacements.Diaphragm is restrained against rotation, therefore θXZ=0.
All diaphragm points, thus also CT, have identical displacements. Diaphragm is restrained against rotation, therefore θXZ=0. Due to zero rotation of diaphragm i, point 1 has only two parallel translations, δYXo=-0.047 and δ YYo=1.668 mm, being identical for all diaphragm points, thus also for CT. As in step 2, in other diaphragms located in the same, upper or lower level small, yet measurable rotations exist, thus every point on them has different displacements. The secondary displacements δXYo of loading 1 and δYXo of loading 3 are always equal, i.e. δXYo=δYXo should always derive from the space frame analysis. Analysis 3 is performed only to obtain translation δYYo needed for the calculation of angle a of the principal system. The angle a of the principal system of diaphragm i is calculated by means of the equation C.9.1 of §C.9 using the 2nd and 3 rd analysis results: tan(2a)=2 δ XYo /( δ XXo - δ YYo )=2 ·(-0.047)/(2.103-1.668)=-0216 → 2a=-12.2º → a=-6.1º Step 4 : Analysis results from loading 1 minus analysis results from loading 2, meaning that only moment and only rotation exists about the centre of stiffness CT, which remains stationary with respect to the ground. .jpg?bhow=0&w=600&h=600&Str=0) Figure D.2-7: The only load acting on diaphragm i is moment on CTDiaphragm displacements are induced only due to rotationThe centre of stiffness CT remains stationary with respect to the ground
Figure D.2-7: The only load acting on diaphragm i is moment on CTDiaphragm displacements are induced only due to rotationThe centre of stiffness CT remains stationary with respect to the ground Figure D.2-7: The only load acting on diaphragm i is moment on CTDiaphragm displacements are induced only due to rotationThe centre of stiffness CT remains stationary with respect to the ground
Diaphragm displacements are induced only due to rotation The centre of stiffness CT remains stationary with respect to the ground Using this trick, namely by subtracting analysis 2 results from analysis 1 results, the diaphragm i develops only rotation, while the remaining diaphragms develop both translations and rotation. However only diaphragm i is examined here. The most important result of this trick is that the diaphragm i is rotated about CT, which remains stationary with respect to the ground, allowing the calculation of its precise location. The rotation angle of diaphragm i is the rotation angle θXZ calculated in step 1 under the corresponding loading.
.jpg?bhow=0&w=600&h=600&Str=0) Figure D.2-8
Figure D.2-8 Figure D.2-8
The displacements of an arbitrary point j of the diaphragm, due to rotation θXZ derive form the expressions: δΧ tj = δ XXj - δ XXo , δ Ytj = δ XYj - δ XYo The CT coordinates corresponding to these displacements are (see §C.5): δΧ t1 = δ XX1 - δ XXo =2.681-2.103=0.578 mm δ Yt1 = δ XY1 - δ XYo =-0.211-(-0.047)=-0.164 mm The diaphragm rotation is identical to that of analysis 1, i.e. θXZ=4.5613·10-5. The coordinates of point 1 are (6.0, 0.0), thus: XCT=X1- δ Yt1 / θ XZ =6.0-(-0.164) ·10-3/(4.5613·10-5)=9.6 m YCT=Y1+ δ Xt1 / θ XZ =0.0+0.578 ·10-3/(4.5613·10-5)=12.7 m Note: To verify the generality of the method, CT coordinates are calculated from point 2 (12.0, 0.0) as well: δΧt2=δXX2-δXXo=2.681-2.103=0.578 mm δYt2=δXY2-δXYo=0.063-(-0.047)=0.110 mm XCT=X2-δYt2/θXZ=12.0-0.110·10-3/(4.5613·10-5)=9.6 m YCT=Y2+δXt2/θXZ=0.0+0.578·10-3/(4.5613·10-5)=12.7 m In the same way, CT coordinates may be verified using any point of the diaphragm. D.3 Diaphragm lateral stiffnesses Each diaphragm has two lateral stiffnesses in the two principal directions. Lateral stiffness of diaphragm Kxx (or Kyy) along the principal x (or y) direction, is defined as the ratio of the seismic force H to the corresponding δxo (or δyo) displacement of the diaphragm, when force acts on CT along the principal direction considered, i.e.: Kxx=Hxx/ δ xxo , Kyy=Hxy/ δ xyo or equivalent: Kxx=Hyx/δyxo , Kyy=Hyy/δ yyo Using analysis 2, the external force HX=100 of the initial system X0Y is resolved into two equivalent principal forces Hxx=100·cosa and Hxy=-100·sina (see §C.2) acting in x,ydirections of the principal system. In the present case, a=-6.154º, therefore Hxx=100·0.994=99.4 kN and Hxy=-100·(-0.107)=10.7 kN. Respectively, the two translations of the centre of stiffness in X0Y, derived from analysis 2, are δXXo=2.103, δΧΥο=-0.047, which transferred in the principal system yield (§C.2): δ xxo = δ XXo · cosa- δ XYo · sina=2.103 ·0.994-(-0.047)·(-0.107)=2.090-0.005=2.085 mm δ xyo =- δ XXo · sina+ δ XYo · cosa=-2.103 ·(-0.107)+(-0.047)·0.994=0.225-0.047=0.178 mm, άρα Kxx=Hxx/ δ xxo =99.4·103N/2.085·10-3m=47.7·106 N/m
Kyy=Hxy/ δ xyo =10.7·103N/0.178·10-3m=60.1·106 N/m
Notes : - If analysis 3 is usedthen:
Hyx=100·sina=-10.7 kN and Hyy=100·cosa=99.4 kN δyxo=δYXo·cosa+δYYo·sina=(-0.047)·0.994+1.668·(-0.107)=-0.047-0.178=0.225, δyyo=-δYXo·sina+δYYo·cosa=-(-0.047)·(-0.107)+1.668·(0.994)=-0.005+1.658=1.653 Kxx=Hyx/δyxo=-10.7·103N/(-0.225·10-3m)=47.6·106 N/m Kyy=Hyy/δyyo=99.4·103N/1.653·10-3m=60.1·106 N/m Namely the same stiffness values are obtained, as expected. - The expressions C.9.2 and C.9.3 of §C.9 could be used for the calculation of stiffnesses Kxx, Kyy, therefore:
Kxx=H/(δXXo+δXYo·tana)=100.0/(2.103-0.047·0.107)·106N/m=47.6·106 N/m
Kyy=H/(δYYo-δXYo·tana)=100.0/(1.668+0.047·0.107)·106N/m=60.0·106 N/m - In case the centres of mass and stiffness coincide, Kxx should be calculated from analysis 2, while Kyy from analysis 3, avoiding division by zero.
D.4 Diaphragm torsional stiffness Torsional stiffness of diaphragm K θis defined as the ratio of moment MCT acting on the centre of stiffness CT, to the rotation angle θ z of the diaphragm.
Moment acting on CT is equal to
MXCT=100.0 · (YCT-YCM)+100.0 · cY=100 · (12.685-12.323)+200.0=36.2+200.0=236.2 kNm
K θ = MXCT/ θ XZ =236.2 ·103 Nm/4.5613 ·10-5=5178·106 Nm
Note: Moment MXCT of external forces is the sum of MXH=36.2 kNm due to external force H and the external moment MXM=200.0 kNm. Respectively, the rotation angle θΧΖ of the diaphragm is the sum of θXZΗ=(MXH/MXCT)·θXZ=(36.2/236.2)· 4.5613·10-5=0.699·10-5 and θXZM=(MXM/MXCT)·θXZ=(200/236.2)· 4.5613·10-5=3.8622·10-5 Also Kθ=MXH/θXZH=MXM/θXZM=5178·106 Nm. The constant moment value in all diaphragms and the respective calculation of torsional stiffness is utilized in the determination of the equivalent system of §D.6. D.5 Torsional stiffness distribution Torsional stiffness distribution of diaphragm is the curve on which, if the idealised columns with the same lateral stiffnesses as those of the diaphragm, are placed symmetrically with respect of the centre of stiffness, the torsional stiffness derived is the same as that of the diaphragm. 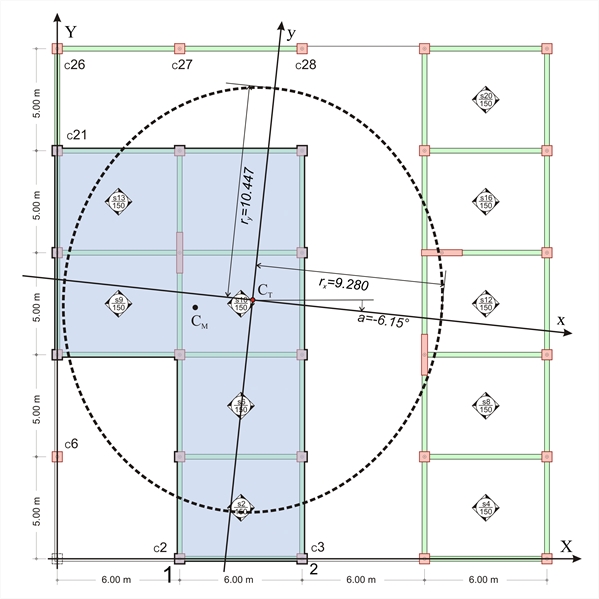 Figure D.5
Figure D.5 Figure D.5
Torsional stiffness ellipse of diaphragmis defined as the ellipse having CT as centre and rx=√(Kθ /Kyy), ry=√(Kθ/Kxx) as radii. rx=√K θ /Kyy=√[5178·106 Ν m/60.1·106N/m]=9.28 m
ry=√K θ /Kxx=√[5178·106Nm/47.7·106N/m]=10.42 m D.6 Equivalent system – Relative lateral stiffness – Relative torsional stiffness A simple, yet equivalent building is created on the basis of appendix Β’, §Β.1 and §Β.2 and the previous paragraphs of the present appendix. The equivalent building should comprise same number of floors and diaphragms. The columns of each floor should have specific dimensions, thus for each floor relative lateral and torsional stiffnesses are used (see §5.4.3.5 and §5.4.4). Each diaphragm is replaced by an equivalent one consisting of 4 fixed-ended columns placed symmetrically with respect to its centre of stiffness. The equivalent diaphragm i is assumed to behave as an one-storey structure of fixed-ended columns. The four relative translations of thecentre of stiffness along X, Y axes δXXoΖ,i, δXYoΖ ,i , δYXoΖ,i, δYYoΖ,i [1] [*] NoteSubscript Z, before, i denotes that the value of the quantity considered is relative rather than absolute. as well as the rotation angle θXZMZ,I are defined as functions of the actual building displacements as follows NoteSubscript Z, before, i denotes that the value of the quantity considered is relative rather than absolute. as well as the rotation angle θXZMZ,I are defined as functions of the actual building displacements as follows δ XXo Ζ ,i = δ XXo,i - δ XXo,i-1 , δ XYo Ζ ,i = δ XYo,i - δ XYo,i-1 ,
δ YXo Ζ ,i = δ YXo,i - δ YXo,i-1 [2] [*] Note Always dXYoZ,i=dYXoZ,i due to δXYo,i=δYXo,i and δXYo,i-1=δYXo,i-1, thus the same is valid for their difference. , δ YYo Ζ ,i = δ YYo,i - δ YYo,i-1 , Note Always dXYoZ,i=dYXoZ,i due to δXYo,i=δYXo,i and δXYo,i-1=δYXo,i-1, thus the same is valid for their difference. , δ YYo Ζ ,i = δ YYo,i - δ YYo,i-1 ,
θ XZ Μ Z,i = θ X ΖΜ ,i – θ XZ Μ ,i-1 [3] [*] Note Subscript M implies rotation angle of the diaphragm due to moment MM=H·c as described in the note of §D.4. . Note Subscript M implies rotation angle of the diaphragm due to moment MM=H·c as described in the note of §D.4. . Therefore, the data of the equivalent diaphragm are: rotation angle az,i=2δXYoΖ,i/( δXXo Ζ,i- δYYoΖ,i), torsional stiffness KθZ,i=H·cY/θXZΜZ,i, lateral stiffnesses KxxZ,i= H/(δXXoZ,i+δXYoZ,i·tana Z,i) and KyyΖ,ι=H/(δYYoZ,i-δXYoZ,i·tanaZ,i) (expressions C.9.2 and C.9.3 of §C.9). Also rxZ,i=√KθZ,i/KyyZ,i, ryZ,i=√KθZ,i/KxxZ,i.
The location of the equivalent diaphragms is determined by translating the centre of stiffness to point 0.0, 0.0. In this way the equivalent building is created and for its diaphragms i the following relations apply: δ XXo_equal,i = Σ ( δ XXo Ζ ,k ) όπου k=i έως 1 → δXXo_equal,i=Σ(δXXo,i-δXXo,i-1)= (δXXo,i-δXXo,i-1)+ (δXXo,i-1-δXXo,i-2)+…+ (δXXo,1-0.0)=δXXo,i → δXXo_equal,i= δXXo,i Using the same logic δXYo_equal,i=δXYo,i , δYYo_equal,i=δYYo,i and θXZ_equal,i= θXZΜ,i Therefore all diaphragm quantities Kxx_equal,i , Kyy_equal,i , Kθ _equal,i are equal to those of the actual building. Two analytical examples for the application of the method are presented in the following paragraph. The seismic assessment of the actual building can be performed in an easy, direct and descriptive way by means of the equivalent building. - In ground floor diaphragms, their torsional stiffness ellipse coincides with the ellipse of the corresponding equivalent diaphragms.
- 1/Kθ_equal,i=Σ(1/KθΖ,j), 1<j ≤ i
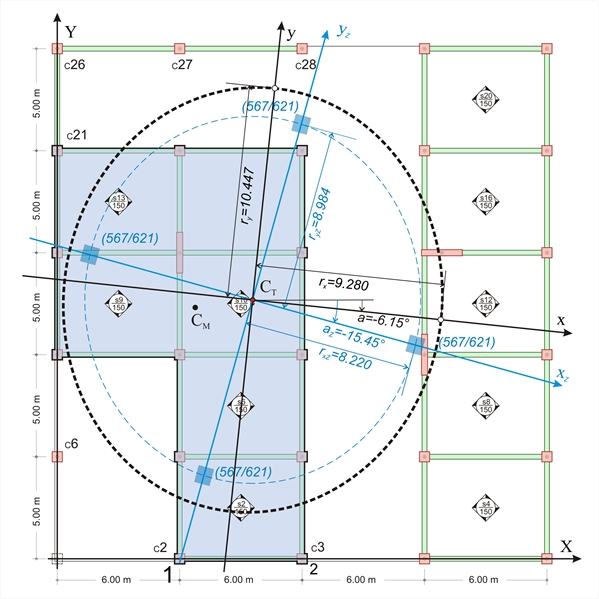 Figure D.6: The equivalent diaphragm of the diaphragm on the left of 4th floor(n=4 equivalent columns of 567/621 cross-section)
Figure D.6: The equivalent diaphragm of the diaphragm on the left of 4th floor(n=4 equivalent columns of 567/621 cross-section) Figure D.6: The equivalent diaphragm of the diaphragm on the left of 4th floor(n=4 equivalent columns of 567/621 cross-section)
(n=4 equivalent columns of 567/621 cross-section) |