Seismic response of buildings Seismic accelerations are induced to the structure by the seismic ground vibration. The seismic response of a structure i.e. its accelerations, induce deformations and stresses. The structural seismic response depends on the following factors: the Seismic Zone the building belongs to, the Importance Factor, the Ground Type, the Viscous Damping, the Behaviour Factor and of course on the magnitude and the distribution of the EI stiffnesses and masses of the building. Hereafter the seismic response factors of buildings are considered. Seismic zones [EC8, §3.2.1] The seismic ground vibration is described by the acceleration agR which denotes the reference peak ground acceleration on type A ground. Each earthquake prone country is divided into Zones depending on the local hazard. A specific reference acceleration agR corresponds to each zone. 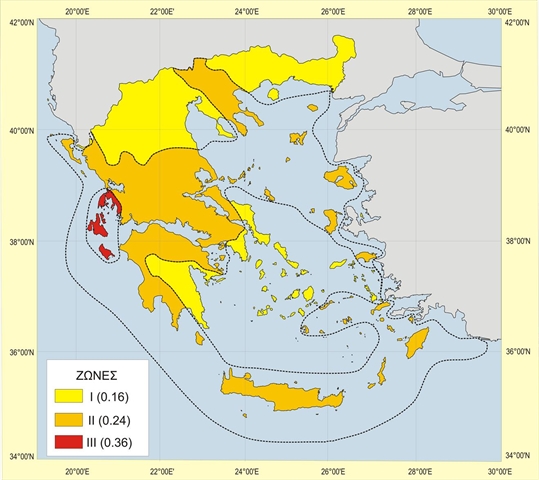 Figure 6.1.1: Map of local hazard seismic zones of Greece
Figure 6.1.1: Map of local hazard seismic zones of Greece Figure 6.1.1: Map of local hazard seismic zones of Greece Importance factors [EC8, §4.2.5] Buildings are classified in four importance classes, depending on the consequences of collapse. Each importance class has an importance factor γI usually varying between 0.80 and 1.40. The design acceleration ag on type A ground derives from the reference acceleration multiplied by the importance factor, i.e.ag =γI· agR | | | | | | | Buildings of minor importance for public safety, e.g. agricultural buildings, etc. | | | | Ordinary buildings, not belonging in the other categories. | | | | Buildings whose seismic resistance is of importance, in view of the consequences associated with a collapse, e.g. schools, assembly halls, etc. | | | | Buildings whose integrity during earthquakes is of vital importance for civil protection, e.g. hospitals, fire stations, power plants, etc. | Table 6.1.2: Importance classes and factors γI for buildings Ground type [EC8, §3.1.2] Ground types are classified in 5 + 2 categories accounting for the influence of local ground conditions on the seismic action. Ground types A, B, C, D, and E, are defined by the stratigraphic profiles and parameters given in the following table. For sites with ground conditions matching either one of the two special ground types S1 or S2, special studies for the definition of the seismic action are required. For these types, and particularly for S2, the possibility of soil failure under the seismic action shall be taken into account. | | Description of stratigraphic profile | | | | | | | | | | Rock or other rock-like geological
formation, including at most 5 m of
weaker material at the surface. | | | | | | Deposits of very dense sand, gravel, or very stiff clay, at least several tens of metres in thickness, characterised by a gradual increase of mechanical properties with depth. | | | | | | Deep deposits of dense or medium-dense sand, gravel or stiff clay with thickness from several tens to many hundreds of metres. | | | | | | Deposits of loose-to-medium cohesion-less soil (with or without some soft cohesive layers), or of predominantly soft-to-firm cohesive soil. | | | | | | A soil profile consisting of a surface alluvium layer with vs values of type C or D and thickness varying between about 5 m and 20 m, underlain by stiffer material with vs > 800 m/s. | | | | | | Deposits consisting, or containing a layer at least 10 m thick, of soft clays/silts with a high plasticity index (PI> 40) and high water content | | | | | | Deposits of liquefiable soils, of sensitive clays, or any other soil profile
not included in types A - E or S1 | | | | Table 6.1.3-1: Ground types The ground type affects the acceleration magnitude, by multiplying them by the soil factor S, whose minimum value is equal to 1.0 for type A ground. It also affects the acceleration distribution, depending on each value of the natural period Τ, and in particular, on thecharacteristic periods TB, TC, TD of the spectrum, that correspond to the specific ground type. The values of S, T B, TC, TD which depend on the ground type are listed in the following table. Table 6.1.3-2: Parameter values describing the recommended Type 1 elastic response spectra [EC8, §3.2.2.2] The viscous damping is accounted for by means of the damping correction factor n determined by the expression:
where ξ is the viscous damping ratio of the structure, expressed as a percentage. The viscous damping ratio is usually taken as being equal to 5%, thus the damping correction factor η is equal to 1.0. |