|
« Modelling slabs using bar and two-dimensional finite elements
Vertical deformation of beams »
|
The frame function in regions of columns The model using both bar and more accurate two-dimensional finite elements, takes into account the slab frame function in regions of columns, in contrast to the inexpensive approach of hinged slab throughout its length. However, in order for the slab to function as a common frame with the columns in the real structure, the slab-to-columns connections (where strong negative bending moments are developed) should be reinforced with strong, correctly placed and well anchored negative reinforcement at the upper fibers of slabs. For this reason, the slab analysis using finite elements in common worksheets should consider hinged supports on columns. 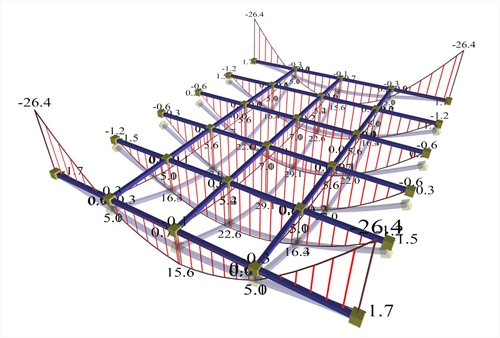 Figure 3.3.6.1-1: Bending moment diagrams of joists of structure modelled with bar finite elements (project <B_336>)
Figure 3.3.6.1-1: Bending moment diagrams of joists of structure modelled with bar finite elements (project <B_336>) Figure 3.3.6.1-1: Bending moment diagrams of joists of structure modelled with bar finite elements (project <B_336>) In case of bar elements, the two main side joists (of slab) forming a common frame with the columns, have greater torsional rigidity than the intermediate nearly hinged main joists and bear heavier loads, thereby to develop strong negative bending moments at their supports and relatively low positive bending moments at their spans. The interim main joists develop strong positive bending moments at their spans, while being supported on the end joists through the secondary joists stressed by significant positive bending moments at their spans. In the more accurate model using two-dimensional finite elements, the main side strips function intensively as frames. Τhe results are similar to those of using bars with the following differences: (a) In the main side strips (corresponding to the main side joists) the frame function is more intensive, since the moments at the supports are greater and moments at the spans are smaller, (b) In the interim main strips (corresponding to the interim main joists) the span moments are smaller, (c) The span moments of the secondary strips (corresponding to secondary joists) end up to be greater. This is due to the fact that the internal torsional stiffness of the slab elements (torsion) is stronger than the respective of bar elements. 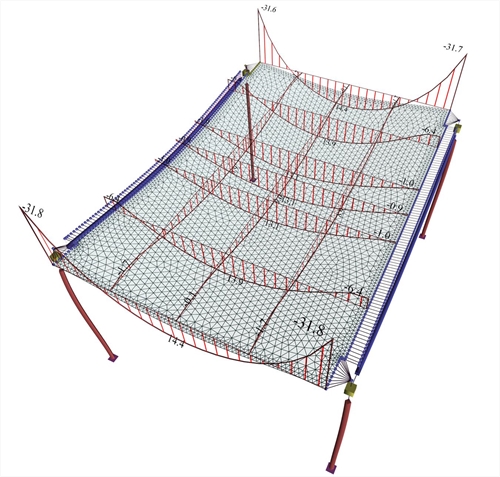 Figure 3.3.6.1-2: Bending moment diagrams of slab strips modelled with triangular finite elements (project <B_336>, pi-FES)
Figure 3.3.6.1-2: Bending moment diagrams of slab strips modelled with triangular finite elements (project <B_336>, pi-FES) Figure 3.3.6.1-2: Bending moment diagrams of slab strips modelled with triangular finite elements (project <B_336>, pi-FES)
|
« Modelling slabs using bar and two-dimensional finite elements
Vertical deformation of beams »
|

|