DIAPHRAGMATIC BEHAVIOUR OF ONE-STOREY SPACE FRAME – GENERAL CASE 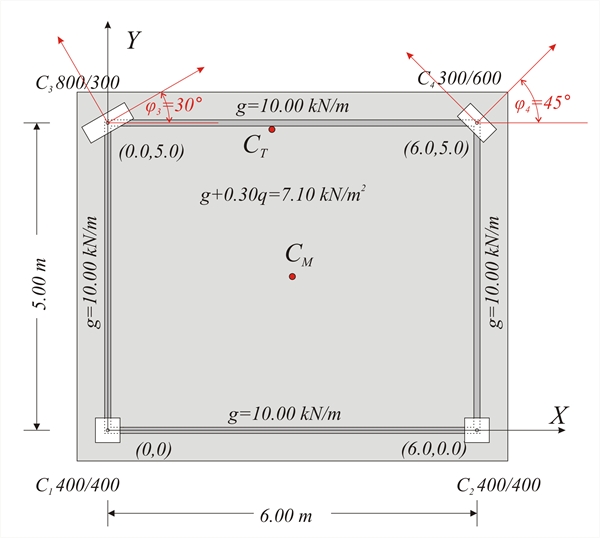 Figure C.1-1: Simple one-storey structure comprising four columns whose tops are connected by a rigid slab-diaphragm.
Figure C.1-1: Simple one-storey structure comprising four columns whose tops are connected by a rigid slab-diaphragm. Figure C.1-1: Simple one-storey structure comprising four columns whose tops are connected by a rigid slab-diaphragm. These rules induce the diaphragm to develop a parallel (translational) displacement by δxo, δyo and a rotationθz about the a point CT(xCT, yCT), the centre of stiffness, in the xCTy coordinate system, which has as origin the point CT and is rotated with respect to the initial coordinate system X0Y by an angle a. To better understand this chapter it is useful to study first §5.4. 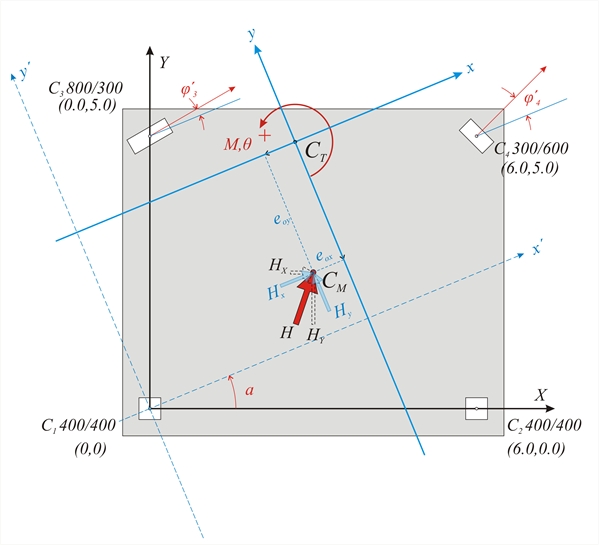 Figure C.1-2
Figure C.1-2 Figure C.1-2 Χ 0Υ initial coordinate system
x’0y’ auxiliary coordinate system
xCTy principal coordinate system 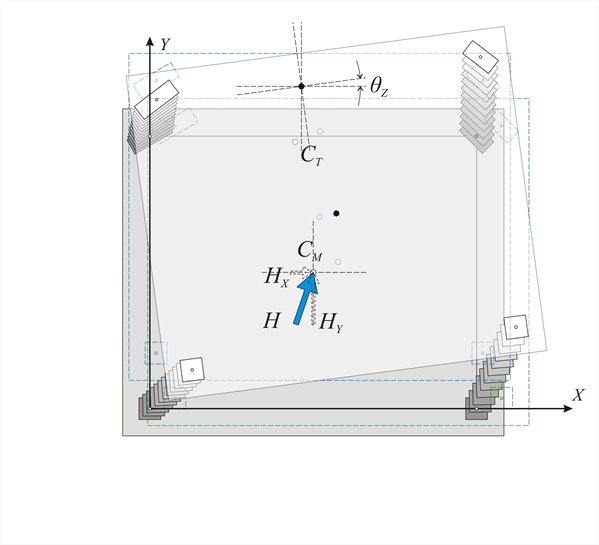 Figure C.1-3: Parallel translation in both directions and rotation of the diaphragm, due to force H
Figure C.1-3: Parallel translation in both directions and rotation of the diaphragm, due to force H Figure C.1-3: Parallel translation in both directions and rotation of the diaphragm, due to force H It is useful to recall the relationship between the two sets of components for the vector v(x,y) transferred from one coordinate system x0y to another ζ0η rotated by an angle φ with respect to the original system. This vector can be either a displacement vector, a force vector, or defining the location of a point. 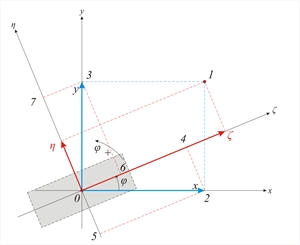 Figure C.2: Relationships of axis transformation due to rotation
Figure C.2: Relationships of axis transformation due to rotation Figure C.2: Relationships of axis transformation due to rotation | ζ =x · cos φ & η =-x · sin φ ζ =y · sin φ & η =y · cos φ | Application of the above relationships on the stiffnesses of a column with cross-section is inclined by an angle φi with respect to the initial system x0y: The displacement of a column top i by δxi is equivalent to the displacements δζ i, δηi in the principal system ζ, η of column i: δζ i = δ xi · cos φ iand δηi=-δxi·sinφ i Displacements δζi and δηi will result in the corresponding shear forces: V ζ i =K ζ i · δ xi · cos φ iand Vηi=-Kηi·δ xi·sinφi. Vxxi=V ζ i · cos φ i -V η i · sin φ i =(K ζ i · δ xi · cos φ i ) · cos φ i -(-K η i · δ xi · sin φ i ) · sin φ i =K ζ i · δ xi · cos2 φ i +K η i · δ xi · sin2 φ i → Vxxi = δ xi · ( K ζ i · cos2 φ i +K η i · sin2 φ i ) Vxyi=V ζ i · sin φ i +V η i · cos φ i =(K ζ i · δ xi · cos φ i ) · sin φ i +(-K η i · δ xi · sin φ i ) · cos φ i =K ζ i · δ xi · (1/2)sin2 φ i -K η i · δ xi · (1/2) · sin2 φ i →
Vxyi= δ xi · (1/2) · ( K ζ i -K η i ) · sin2 φ i In a simpler form, these two expressions, as a function of the normalised stiffness coefficients, of column i in direction x, Kxxi and Kxyi, are: Vxxoi= δ xi × Kxxiwhere Kxxi= Kζi×cos2φi +Kηi×sin2φi (a) Vxyoi= δ xi × Kxyiwhere Kxyi=(1/2)×(Kζi-Kη i)×sin2φi (b) Quantities Kxxi and Kxyi are called normalised stiffnesses of column i in direction x. In a similar way, the expressions as a function of the normalised stiffness coefficients Kyxi and Kyyi of column in direction y are: Vyxoi= δ yi × Kyxiwhere Kyxi=(1/2)×(Kζi-Kη i)×sin2φi= Kxyi (c) Vyyoi= δ yi × Kyyiwhere Kyyi=Kζi×sin2φi +Kηi×cos2φi (d) - In every coordinate system, for each column i always Kxyi=Kyxi.
- Stiffness coefficients Kxxi, Kxyi and Kyyi are identical in all systems parallel to x0y, therefore to x’0y’ as well.
- In rectangular columns the angle φ is irrelevant since Kζ=Kη therefore (a) and (d) always give Kxx=Kyy =Kζ=Kη and (b) always gives Kxy=0.
The columns of the example have the same E and h, therefore their stiffness can be assumed as Κ ji =C × Iji where C=12E/h3 As elasticity modulus is assumed Ε =32.80 GPa corresponding to concrete C30/37 (§6.1) therefore C=12E/h3=12 × 32.80 × GPa/(3.03m3)=14.58 × 109N/m5 . Column stiffnesses with respect to their local coordinate systems ζ , η : C 1 , C 2 400/400 K ζ1 = K 1η = K 2ζ = K 2η =14.58·109 N / m 5 × 0.400 × 0.4003/12 × m 4 =31.1 × 106 N / m , C 3 800/300 K 3ζ =14.58 × 109 × 0.300 × 0.8003/12=186.6 × 106 N / m , K 3η =14.58 × 109·0.800 × 0.3003/12=26.2 × 106 N / m C 4 300/600 K 4ζ =14.58 × 109 × 0.600 × 0.3003/12=19.7 × 106 N / m , K 4η =14.58 × 109 × 0.300 × 0.6003/12=78.7 × 106 N / m The diaphragmatic behaviour may be considered as superposition of three cases: (a) parallel translation of the diaphragm in X direction due to horizontal force component HX, (b) parallel translation of the diaphragm in Y direction due to horizontal force component HY, (c) rotation of the diaphragm due to moment MCT applied at the centre of stiffness CT The horizontal seismic forces are applied at each point with mass, while the resultant force is applied at the centre of mass CM. In case the direction of the force H passes through the point CT as well as CM the moment has zero value and therefore the diaphragm develops zero rotation. C.3 Case 1: Translation of centre of stiffness CT along x direction by δxο 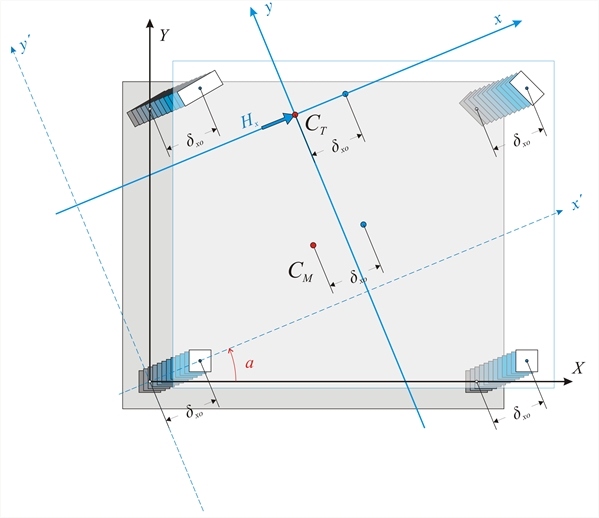 Figure C.3
Figure C.3 Figure C.3 When a horizontal force Hx acts on the CT along the x direction, the 3 following equilibrium equations should apply: - The sum of forces acting in x direction is be equal to Hx, i.e. Hx=Σ (Vxxoi) (i)
- The sum of forces acting in y direction is equal to zero, i.e. Σ(Vxyoi)=0.0 (ii)
- The sum of moments Vxxoi and Vxyoi about point CT is equal to zero,
i.e. Σ(Vxxoi·yi-Vxyoi· xi)=0 (iii) where Vxyoi=δxo×Kxyi with Kxyi=1/2×(Kζi-Kηi)×sin2φ’i and φ’i=φi -a Expression (i) yields Hx=Σ(δxo× Kxxi)=δxo×Σ(Kxxi) →
Because of the identity sin ( w 1 - w 2 )=sin w 1 · cos w 2 -cos w 1 · sin w 2, Kxyi=1/2·(Kζi-Kηi)·(sin2φi·cos2a-cos2φi·sin2a) equation (ii) becomes Σ(Kxyi)=0 → Σ[(Kζi-Kηi)·sin2φi·cos2a]=Σ[(Kζi-Kηi)cos2φi·sin2a] → cos2a·Σ[(Kζi-Kηi)·sin2φi]=sin2a·Σ[(Kζi-Kηi)·cos2φ i] → Calculation of angle a of the principal system : Using the same values for K ζ , K η previously calculated and since 2 φ 1 =2 φ 2 =0˚, 2 φ 3 =60˚ and 2 φ 4 =90˚: (3) → tan2a=Σ[(Kζi-Kηi)×sin2φi]/Σ[(Kζi-Kηi)×cos2φi ] → tan2a=[(31.1-31.1) × 106 × sin0˚ +(31.1-31.1) × 106 × sin0˚+(186.6-26.2) × 106 × sin60˚+ (19.7-78.7) × 106 × sin90˚]/ /[( 31.1-31.1) × 106 × cos0˚+(31.1-31.1) × 106 × cos0˚ + (186.6-26.2) × 106 × cos60˚+ (19.7-78.7) × 106·cos90˚]=[0+0+138.9-59.0]/[0+0+80.2+0.0]=79.9/80.2=0.996 → 2a=44.88˚ → a=22.44˚ Therefore the angle of the principal system is a=22.44˚ Coordinate system transformation : From the initial system X0Y we are transferred to the auxiliary x’0y’, which is parallel to the principal system xCTy, therefore angle of the initial system is a=22.4˚: C1: from C1(0,0) and φ 1 =0˚ becomes C1(0,0) φ ’1=-22.44˚ C2: from C2(6.0,0) and φ 2 =0˚ becomes C2(6.0 ×0.924=5.544, -6.0×0.3817=-2.290), φ’2=-22.44˚ C3: from C3(0.0,5.0) and φ 3 =30˚ becomes C3(5.0×0.3817=1.9085, 5.0×0.924=4.62), φ’3=30˚-22.44˚ =7.56˚ → C3(5.544, -2.290), φ’3=7.56˚ C4: from C4(6.0, 5.0) and φ 4 =45˚ becomes C4(6.0×0.924+5.0×0.3817=7,4542, -6.0×0.3817+5.0×0.9243=2.331), φ’4=45˚-22.44˚ =22.56˚ → C4(7.454, -2.331), φ’4=22.56˚ CM: from CM(3.0, 2.5) becomes CM(3.0 ×0.924+2.5×0.3817=3.727, -3.0×0.3817+2.5×0.9243=1.166) Working on the auxiliary coordinate system x’0y’ xi=x’i-x’CT and yi=y’i-y’CT therefore equation (iii) yields: δ xo × Σ ((y’i-yo) × Kxxi-(x’i- x’CT) × Kxyi)=0 → Σ (y’i × Kxxi)-yo × Σ (Kxxi)- Σ (x’i × Kxyi)+ x’CT · Σ (Kxyi)=0 → Σ ((x’i- x’CT) × Kyyi-(y’i- y’CT) × Kxyi)=0 → - Σ (y’i × Kxyi)+ y’CT × Σ (Kxyi)+ Σ (x’i × Kyyi)- x’CT × Σ (Kyyi)=0. Since Σ(Kxyi)=0, Σ(y’i×Kxxi)- y’CT×Σ(Kxxi)-Σ(x’i×Kxyi)=0 → - Σ (y’i × Kxyi)+ Σ (x’i × Kyyi)- x’CT × Σ (Kyyi)=0 →
C.4 Case 2: Translation of centre of stiffness CT along direction y by δyο  Figure C.4
Figure C.4 Figure C.4 Accordingly, taking into account that Kyxi=Kxyi, the corresponding expressions are: Since C1, C2 have a square cross section → Kxx1=Kyy1=Kxx2=Kyy2=31.1·106 N/m, Kxy1=Kxy2=0.0 C3: φ ’3=7.56˚ (a) → Kxx3= Kζ3·cos2φ3+Kη3·sin2φ3 =[186.6·0.99132 +26.2·0.13162]·106=183.82· 106 N/m (b)→ Kxy3=(1/2)·(Kζ3-Kη3)·sin2 φ3=0.5·(186.6-26.2)· 106 ·0.261=20.93·106 N/m (d) → Kyy3= Kζ3·sin2φi+Kη3·cos2φ3 =[186.6·0.13162 +26.2·0.99132] ·106 N/m =28.98·106 N/m C4: φ ’4=22.56˚ (a) → Kxx4=Kζ4·cos2φ4+Kη4·sin2φ4=[19.7·0.92352+78.7·0,38372] ·106=28.39·106 N/m (b)→ Kxy4=(1/2)·(Kζ4-Kη4)·sin2φ4 =0.5·(19.7-78.7)·106·0.709=-20.92·106 N/m (d) → Kyy4= Kζ4·sin2φi+Kη4·cos2φ3 =[19.7·0,38372+78.7·0.92352] ·106=70.02·106 N/m Total stiffnesses of the diaphragm and structural moments of the stiffnesses with respect to CT : Kxx= Σ (Kxxi)=( 31.1+31.1+183.82+28.39) ·106=274.41·106 N/m Kyy= Σ (Kyyi)= (31.1+31.1+28.98+70.02) ·106=161.2·106 N/m Σ (x’i·Kyyi)=[0.0·31.1+5.544·31.1+1.9085·28.98+7.4542 ·70.02]·106 =749.55·106 N Σ (x’i·Kxyi)=[0.0·0+5.544·0+1.9085·20.93+7.4542 ·(-20.93)]·106=-116.07·106 N Σ (y’i·Kxxi)=[0.0·31.1-2.29·31.1 +4.62·183.82+2.331 ·28.39]·106=844.21·106 N Σ (y’i·Kxyi)= [0.0·0.0 -2.29·0.0 +4.62·20.93+2.331 · (-20.92)]·106=47.93·106 N x’CK=[ Σ (x’i·Kyyi)- Σ (y’i·Kxyi)]/ Σ (Kyyi)=( 749.55-47.93)/161.2=4.353 m y’CK=[ Σ (y’i·Kxxi)- Σ (x’i·Kxyi)]/ Σ (Kxxi)=( 844.21+116.07)/274.41=3.500 m C.5 Case 3: Rotation of the diaphragm by an angle θz about CT 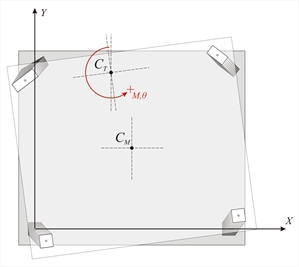 Figure C.5-1: Displacements of a random point i of the diaphragm due to rotation by θz
Figure C.5-1: Displacements of a random point i of the diaphragm due to rotation by θz Figure C.5-1: Displacements of a random point i of the diaphragm due to rotation by θz |  Figure C.5-2: Displacements due to rotation from a moment M applied in CT
Figure C.5-2: Displacements due to rotation from a moment M applied in CT Figure C.5-2: Displacements due to rotation from a moment M applied in CT δ xi =-ri· θ z ·yi/ri=-yi· θ z | Consider the principal coordinate system xCTy The deformation induced by the external moment M applied in CT , is examined. In order to examine this deformation a transfer is needed from the auxiliary system x’0y’ to the principal system xCTy by a simple parallel translation. By alsotransferring the centre of mass in the principal system as well, the structural eccentricities eox, eoy of CM with respect to CT, derive from the expressions:
The deformation of the diaphragm is a rotation θz about CT. Rotation θzof diaphragm induces a displacement δi at the top of each column i with coordinates xi,yi with respect to the coordinate system having as origin CT. If the distance of point ifrom CT is ri, the two components of the (infinitesimal) deformation δi are: δxi=-θz×yi and δyi = θz×xi Coordinate transfer in the principal system and calculation of the structural eccentricities : C1(0.0-4.353=-4.35, 0.0-3.500=-3.50) φ ’1=-22.44˚ Kxx=31.1 ×106, Kyy=31.1×106, Kxy=0.0 C2(5.544-4.353=1.19, -2.290-3.500=-5.79), φ ’2=-22.44˚ Kxx=31.1 ×106, Kyy=31.1×106, Kxy=0.0 C3(1.9085-4.353=-2.44, 4.62-3.500=1.12), φ ’3=7.56˚ Kxx=183.82, Kyy=28.98, Kxy=20.93 C4(7,4542-4.353=3.10, 2.3312-3.500=-1.17), φ ’4=22.56˚ Kxx=28.39, Kyy=70.02, Kxy=-20.92 CM(3.727-4.353=-0.626, 1.166-3.500=-2.334) and obviously CT(0,0) eox=-0.626 m, eoy=-2.334 m Displacements δxi, δyi incuce shear forces Vxi and Vyi in each column: Vxi=Kxxi × δ xi = Kxxi × (- θ z × yi ) →Vxi= -θz×Kxxi×yi and Vyi=Kyyi×δyi=kyyi×θz×xi → Vyi=θz× kyyi×xi The resultant of the moments of all shear forces Vxi, Vyi with respect to the CT should be equal to the external moment MCT i.e.: MCT= Σ [-Vxi × yi + Vyi × xi+Kzi] → MCT= θ z × Σ [Kxxi × yi2 + Kyyi × xi2+Kzi] →
Calculation of diaphragm torsional stiffness : Κθ = Σ (Kxxi × yi2+Kyyi × xi2+Kzi)= Σ [31.1×3.52+31.1×4.352+31.1×5.792+31.1×1.192+183.82×1.122+ 28.98×2.442+28.39×1.172+70.02×3.102]×106 N×m= =[381.0+588.5+1042.6+44.0+230.6+172.5+38.9+672.9] ×106 N×m → Κθ=3174×106 N×m The quantity Κθ=Σ(Kxxi×yi2 + Kyyi ×xi2+Kzi) is called torsional stiffness of the diaphragm, measured in units ofmoment e.g. N×m, by analogy with the quantities Kx=Σ(Kxi), Ky=Σ(Kyi) which are called lateral stiffnesses of the diaphragm in direction x and y respectively and measured in N/m. The torsional stiffness of the column itself is usually insignificant and can be ignored (§5.4.3.4). Lateral stiffness Κ jk of diaphragm denotes the force in j direction required to cause displacement of the diaphragm by one unit in the k direction. Torsional stiffness Κθ of diaphragm denotes the moment required to cause rotation of the diaphragm by one unit. C.6 Torsional stiffness ellipse, torsional radii and equivalent system Question: Create a simple idealised equivalent structural system with the same seismic behaviour as the actual structural system. Solution: Four idealised columns E1, E2 and E3, E4 are placed symmetrically with respect to the centre C T and to the axes x and y, i.e. all four idealised columns have x and y coordinates with the same absolute values. Each idealised column isassumed to have a stiffness equal to Kx=1/4×Σ(Kxi) and Ky=1/4 ×Σ(Kyi). 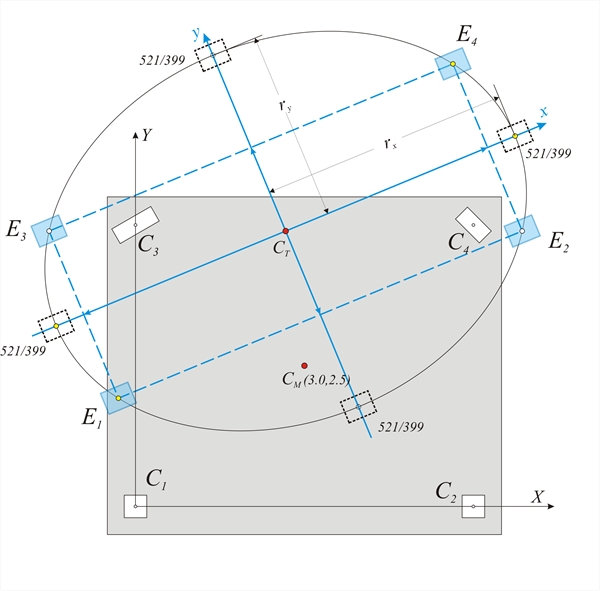 Figure C.6
Figure C.6 Figure C.6 This system satisfies the two conditions of the actual system, concerning the translations of all diaphragm columns since: Stiffness by x: 4×1/4×Σ(Kxi)=Σ(Kxi) and stiffness by y: 4×(1/4) ×Σ(Kyi)=Σ(Kyi). To satisfy the third condition, the torsional stiffness of the idealised system should be K θ ,eq =[Kx1 × y2+Kx2 × y2+Ky1 × x2+Ky2 × x2]= Σ (Kxxi) × y2+ Σ (Kyyi) × x2 equal to the torsional stiffness of the actual system K θ ,re =K θ = Σ (Kxxi·yi2 + Kyyi·xi2 -2Kxyi·xi·yi+Kzi) , i.e. should Kθ,eq= Kθ,re → Σ(Kxxi)·y2+Σ(Kyyi)·x2=Kθ →
The curve equation (8) is an ellipse with centre CT and semiaxes rx, ry oriented along the principal axes Calculation of the torsional stiffness ellipse rx=√(K θ /Kyy)=√(3134·106N·m / 161.2 ·106N/m)=4.41 m ry=√(K θ /Kxx)=√(3134·106 N·m / 274.41 ·106N/m)=3.38 m The torsional behaviour of a floor can be described by the torsional stiffness ellipse (CT, rx, ry) which represents the equivalent distribution of the diaphragm stiffness. The radii rx, ry, of the ellipse are called torsional radii. There are infinite solutions of idealised dual system sets, whose most characteristic is the one with the four idealised columns placed in the four ellipse ends. Generally, there are infinite solutions with n-tuple diametrically opposed systems, where each idealised column stiffness is equal to 1/n of the total system stiffness. - The torsional stiffness ellipse is better to enclose the mass inertial ring
- The position of ‘walls’ is not significant, provided they are located as close as possible to the perimeter. It is significant, however, to have high stiffness in both directions.
- Significant deviation between CM and CT can be handled by placing walls of high stiffness in the perimeter of the building.
C.7 Superposition of the three cases So far, all the calculations depended on the structure geometry and were not affected by the magnitude of the external loading. For instance the centre of stiffness, the structural eccentricities, and the torsional radii, are independent of the seismic force magnitude. Next, the displacements and stress resultants of the structure, due to external seismic loading H, will be calculated. The relevant seismic force H is applied at the centre of mass CM of the diaphragm. This force is resolved in two forcesHx and Hy parallel to the two axes of the principal system. In order to apply the previous analysis, the forcesHx, Hy are transferred to the centre of stiffness CT together with the moment MCT according to the expression:
Calculation of moment MCT : The structural eccentricities are eox =-0.626 and eoy= yCM=-2.334m For a given force Η =HX=90.6 kN in the initial system X0Y, the equivalent loading in the principal system (a=22.44 ο ) is: Hx=HX × cosa=90.6 ×0.924=83.72 kN and Hy=-HX×sina=-90.6×0.382=-34.64 kN and Μ CT =-Hx × eoy+Hy × eox=-83.72kN × (-2.334m)+[-34.64kN × (-0.626m)]=195.4 kNm+21.7kNm=217.1 kNm The following quantities are calculated using the Hx, Hy, MCT: - the displacements δxo, δyo and θ z of CT using the expressions:
Quantities Kxx= Σ (Kxxi)= 161.2 × 106N/m, Kyy= Σ (Kyyi)= 161.2 × 106 N/m and Κθ =3134 × 106 N × m are already calculated therefore: δ xo =Hx/ Κ xx =83.72 × 103N/(274.41 × 106N/m)=0.305 mm, δ yo =Hy/ Κ yy =-34.46 × 103N/(161.2 × 106 N/m)=- 0.214 mm and θ z =MCT/K θ =217.1kNm/(3134·103kNm)=0.692·10-4 - the displacements δxi, δyi of the top of each column using the expressions:
- and the displacements δζi, δηi by transferring δxi, δyi to the local system of each column using the expressions:
C1: δ x1 = δ xo - θ z × y1=0.305mm-0.692 × 10-4·(-3.50 × 103mm)=(0.305+0.242)mm=0.547 mm δ y1 = δ yo + θ z × x1=-0.214mm+0.692 × 10-4·(-4.35 × 103mm)=(-0.214-0.301)mm=-0.515 mm By transferring to the local system where φ ’1=0.0-22.44 ° =-22.44 °. δζ 1 = δ x1 × cos φ ’1+ δ y1 × sin φ ’1=0.547 ×0.924-0.515×(-0.382)=0.505+0.197=0.702 mm δη 1 =- δ x1 × sin φ ’1+ δ y1 × cos φ ’1=-0.547 ×(-0.382)+(-0.515)×0.924=0.209-0.476=-0.267 mm C2: δ x2 = δ xo - θ z × y2=0.305mm-0.692 × 10-4·(-5.79 × 103mm)=(0.305+0.400)mm=0.705 mm δ y2 = δ yo + θ z × x2=-0.214mm+0.692 × 10-4 × 1.19 × 103mm=(-0.214+0.082)mm=-0.132 mm By transferring to the local system where φ ’2=0.0-22.44 ° =-22.4 °. δζ 2 = δ x2 × cos φ ’2+ δ y2 × sin φ ’2=0.705 ×0.924+(-0.291)×(-0.132)=0.652+0.038=0.701 mm δη 2 =- δ x2 × sin φ ’2+ δ y2 × cos φ ’2=-0.705 ×(-0.382)+(-0.132)×0.924=0.269-0.122=0.147 mm C3: δ x3 = δ xo - θ z × y3=0.305mm-0.692 × 10-4 × 1.12 × 103mm=(0.305-0.078)mm=0.227 mm δ y3 = δ yo + θ z × x3=-0.214mm+0.692 × 10-4 × (-2.44 × 103mm)=(-0.214-0.169)mm=-0.383 mm By transferring to the local system where φ ’3=30.0-22.44 ° =7.56 °. δζ 3 = δ x3 × cos φ ’3+ δ y3 × sin φ ’3=0.227 ×0.991+(-0.383)×0.132=0.225-0.050=0.175 mm δη 3 =- δ x3 × sin φ ’3+ δ y3 × cos φ ’3=-0.227 ×0.132+(-0.383)×0.991=-0.030-0.380=-0.410 mm C4: δ x4 = δ xo - θ z × y4=0.305mm-0.692 × 10-4 × (-1.17·103mm)=(0.305+0.081)mm=0.386 mm δ y4 = δ yo + θ z × x4=-0.214mm+0.692 × 10-4 × 3.10 × 103mm=(-0.214+0.215)mm=0.001 mm By transferring to the local system where φ ’4=45.0-22.44 ° =22.56 °. δζ 4 = δ x4 × cos φ ’4+ δ y4 × sin φ ’4=0.386 ×0.923+0.001×0.384=0.355+0.000=0.355 mm δη 4 =- δ x4 × sin φ ’4+ δ y4 · cos φ ’4=-0.386 ·0.384+0.001·0.923=-0.148+0.001=-0.147 mm In the example considered, for seismic action in X direction, the deformation due to rotation at column C2 gives δ x2, θ =0.400 mm, higher than the deformation due to translation δ xo =0.305 mm. The total displacement is therefore δ x2 =0.305+0.400=0.705 mm. -
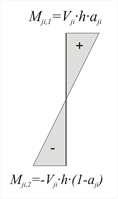 Figure C.7: Moment distribution (Mji,1- Mji,2=Vji×h)
Figure C.7: Moment distribution (Mji,1- Mji,2=Vji×h) Figure C.7: Moment distribution (Mji,1- Mji,2=Vji×h)
Calculation of shear forces and bending moments : C1: V ζ 1 = δζ 1 · K ζ 1 =0.702mm · 31.1 · 106 N/m =21.8 kN V η 1 = δη 1 · K η 1 =-0.267mm · 31.1 · 106 N/m =-8.3 kN M ζ 1,1 =V ζ 1 · h · 0.50=21.8·3.0·0.50=32.7 kNm Mζ1,2=- Mζ1,1 =-32.7 kNm M η 1,1 =V η 1 · h · 0.50=-8.3·3.0·0.50=-12.5 kNm Mηι,2=- Mη1,1 =12.5 kNm C2: V ζ 2 = δζ 2 · K ζ 2 =0.701mm · 31.1 · 106 N/m =21.8 kN V η 2 = δη 2 · K η 2 =0.147mm · 31.1 · 106 N/m =4.6 kN M ζ 2,1 =V ζ 2 · h · 0.50=21.8·3.0·0.50=32.7 kNm Mζ2,2=- Mζ2,1 =-32.7 kNm M η 2,1 =V η 2 · h · 0.50=4.6·3.0·0.50=6.9 kNm Mη2,2=- Mη2,1 =-6.9 kNm C3: V ζ 3 = δζ 3 · K ζ 3 =0.175mm · 186.6 · 106 N/m =32.7 kN V η 3 = δη 3 · K η 3 =-0.410mm · 26.2 · 106 N/m =-10.8 kN M ζ 3,1 =V ζ 3 · h · 0.50=32.7·3.0·0.50=49.1 kNm Mζ3,2=- Mζ3,1 =-49.1 kNm M η 3,1 =V η 3 · h · 0.50=-10.8·3.0·0.50=-16.2 kNm Mη3,2=- Mη3,1 =16.2 kNm C4: V ζ 4 = δζ 4 · K ζ 4 =0.355mm · 19.7 · 106 N/m =7.0 kN V η 4 = δη 4 · K η 2 =-0.147mm · 78.7 · 106 N/m =-11.6 kN M ζ 4 =V ζ 4 · h · 0.50=7.0·3.0·0.50=10.5 kNm Mζ4,2=- Mζ4,1 =-10.5 kNm M η 4,1 =V η 4 · h · 0.50=-11.6·0·0.50=-17.4 kNm Mη4,2=- Mη4,1 =17.4 kNm
GEOMETRIC DATA OF THE DIAPHRAGM (independent of the loading) 2. Calculation of angle a of the main system using expression (3) 3. Calculation of column angles φ ’i in the principal system x,y using the expression φ ’i= φ i -a 4. Calculation of column stiffnesses Kxxi, Kxyi, Kyyi in the principal system x,y using expressions (a), (b), (c) 5. Calculation of each column centre of gravity and centre of mass (x’CM, y’CM) using the relationships for the transformation from the principal system X0Y to the auxiliary system x’0y’. 6. Calculation of diaphragm total stiffnesses using the expressions Kx= Σ (Kxxi), Ky= Σ (Kyyi). Calculation of the quantities Σ (x’i · Kyyi), Σ (y’i · Kxyi), Σ (y’i · Kxxi), Σ (x’i · Kxyi) and the coordinates of the centre of stiffness CT(x’CT, y’CT) using the expressions (4) and (5) 7. Transfer of the coordinates x’, y’ of the diaphragm CM and each column centre of gravity in the principal system. Calculation of the structural eccentricities eox, eoy using the expressions (6’). 8. Calculation of torsional stiffness K θ using the expression (7) 9. Calculation of torsional radii rx, ry using the expressions (8) Up to this point the calculations are independent of the external loading. Next, the stress distribution and the elastic deformations of the diaphragm elements, due to the external loading, are calculated. FLOOR DISPLACEMENTS AND STRESS RESULTANTS (dependent on the loading) 10. Transfer of horizontal forces Hx, Hy and moment MCT to the CT using the expression (9). 11. Calculation of displacements δ xo , δ yo and θ z of the CT using the expressions (10). 12. Calculation of the displacements δ xi , δ yi of each column top using the expressions (11). 13. Calculation of the corresponding displacements δζ i , δη i in the local system of each column using the expressions (12) 14. Calculation of principal shear forces V ζ i , V η i of each column using the expressions (13) 15. Calculation of principal bending moments M ζ i,1 , M ζ i,2 & M η i,1 , M η i,2 using the expressions (14)
C.9 Expressions relating the initial system X0Y and the principal system xCTy Seismic force Η X =H acting in X direction (HΥ=0) in the initial system X0Y: The equivalent forces Hx, Hy in the principal system xCTy are: Hx=H·cosa and Hy=-H·sina and the equivalent deformations of CT, δx, δy, in the principal system are: δx = δXXο·cosa + δΧΥο·sina and δy=- δXX ο·sina +δΧΥο·cosa. Hx=Kxx ·δ x and Hy=Kyy·δy therefore: H · cosa = Kxx · ( δ XX ο · cosa + δΧΥο · sina) → H=Kxx·( δXXο+tana· δΧΥο) (i) -H · sina = Kyy · (- δ XX ο · sina + δΧΥο · cosa) →-tana·H=Kyy·(-tana·δXX ο+δΧΥο) (ii) Seismic force Η Y =H acting in Y direction (HX=0) in the initial system X0Y: The equivalent forces Hx, Hy in the principal system xCTy are: Hx=H·sina and Hy=H·cosa and the equivalent deformations of CT, δx, δy,in the principal system are: δ x = δΧΥο · cosa+ δ YYo · sina and δy =-δYXo·sina+ δ YYo·cosa. Hx=Kxx · δ x and Hy=Kyy·δy due to δ YXo = δΧΥο yields: H · sina=Kxx · ( δΧΥο · cosa+ δ YYo · sina) → tana·H=Kxx·( δΧΥο+tana ·δYYo) (iii) H · cosa=Kyy · (- δΧΥο · sina+ δ YYo · cosa) → H=Kyy·(-tana·δΧΥο+δ YYo) (iv) (iv) → Kyy=H/(δYYo - tana·δΧΥο) (i) → Kxx=H/(δXXο + tana·δΧΥο) (iii) → tana·H= H/( δXXο+tana·δΧΥο)·( δΧΥο+tana·δ YYo) → tana · ( δ XX ο +tana · δΧΥο )= δΧΥο +tana · δ YYo ) → tana·δXXο +tan2a· δΧΥο = δΧΥο +tana·δYYo → δΧΥο · (1- tan2a)=tana · ( δ XX ο - δΧΥο )→ δΧΥο=[tana/(1- tan2a)]·( δXX ο - δYYo) → tan2a = 2 δΧΥο / ( δ XX ο - δ YYo ) (C.9.1) Kxx=H/( δ XX ο +tana · δΧΥο ) (C.9.2) Kyy=H/( δ YYo -tana · δΧΥο ) (C.9.3) Κθ =H · (YCT-YCM)/ θ xz (C.9.4) C.10 One-storey space frame with rectangular columns in random arrangement The method which describes the diaphragmatic behaviour of each floor is presented in Appendix D. Also relevant examples are presented verifying the validity of the algorithms of the general method. The analysis of the one-storey space frame illustrated in the figure, under horizontal seismic force H=90.6 kN is performed by means of four methods: (i) analysis using manual calculations, assuming fixed-ended columns, (ii) analysis using the Excel file, assuming fixed-ended columns, (iii) analysis using the Excel file, assuming columns with k=6, (iv) assuming using software, assuming actual beam and column torsional stiffnesses. 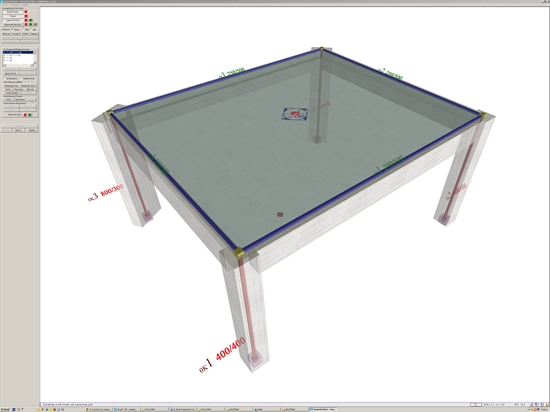 Figure C.10: Frame and model of a single-storey space frame
Figure C.10: Frame and model of a single-storey space frame Figure C.10: Frame and model of a single-storey space frame
The names, loadings, coordinates and dimensions of slabs and columns are shown in figure of §C.1. The cross-section of beams is 250/500. The concrete class is C30/37 (Ε=32.80 GPa). C.10.1 Analysis using manual calculations, assuming fixed columns (k=12) This method was described via the example presented to all previous paragraphs of this appendix. C.10.2 Analysis using the Excel file, assuming fixed-ended columns (k=12) The related <diaphragm_general.xls> spreadsheet is used assuming fixed-ended columns. 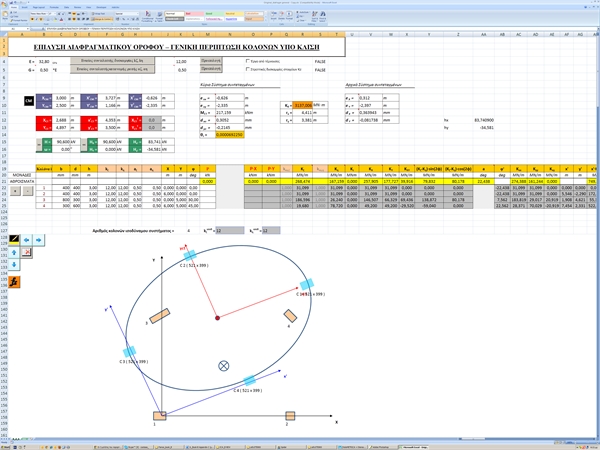 Figure C.10.2: The results are identical to those of the practical calculations.The torsional stiffness ellipse and the equivalent columns of the structure are drafted at the end of the spreadsheet.
Figure C.10.2: The results are identical to those of the practical calculations.The torsional stiffness ellipse and the equivalent columns of the structure are drafted at the end of the spreadsheet. Figure C.10.2: The results are identical to those of the practical calculations.The torsional stiffness ellipse and the equivalent columns of the structure are drafted at the end of the spreadsheet. The torsional stiffness ellipse and the equivalent columns of the structure are drafted at the end of the spreadsheet. C.10.3 Analysis using the Excel file, assuming columns with k=6 The centre of stiffness, the torsional radii and the stress resultants derived from this method are exactly the same as those of the previous methods, with the exception of deformations, whose their relative values, however, remain constant 12/6=2.00. C.10.4 Analysis using software, assuming actual beam and column torsional stiffnesses In order to define the diaphragmatic function of a building’s storey, with actual stiffness and not with assumption of fixed function of its columns, it is necessary to use the appropriate software. Structural analysis software is necessary for one storey, as well as multistorey buildings, even in case of rectangular columns in parallel arrangement. The method which describes the diaphragmatic behaviour of each floor is presented in Appendix D and this example is analysed as example 1. |