Fundamental support and span moments - Deflection curves Two calculation methods are: Marcus method and Czerny method. In this method, the slab is replaced by two intersecting strips along directions x and y respectively, which meet in its middle point m. Depending on the support conditions, the strips are classified as simply supported, fixed at one end or fixed at both ends. Each strip, subjected to its corresponding load, provides an elastic line and a bending moment diagram: 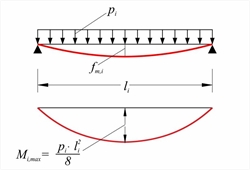 Simply supported strip
Simply supported strip Simply supported strip
 Strip fixed at one end
Strip fixed at one end Strip fixed at one end
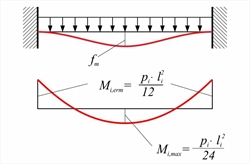 Figure 4.6.2.1: Strip fixed at both ends
Figure 4.6.2.1: Strip fixed at both ends Figure 4.6.2.1: Strip fixed at both ends
Each strip bears load px ή py such as:
Loads px=kx·p and py=ky·p (kx+ky=1.00) are calculated according to equations (1) and (2), where:
[*] Notef0m=cx·px·l4x/(E·I)=12·cx·kx·l4x/(E·b·h3)=aom·l4x/(E·1.0·h3), where a om=12·cx·kx Notef0m=cx·px·l4x/(E·I)=12·cx·kx·l4x/(E·b·h3)=aom·l4x/(E·1.0·h3), where a om=12·cx·kx
The bending moments on the spans and the supports are calculated by analyzing simply supported, fixed at one end or fixed at both ends strips, subjected to load px and py in both directions respectively. The consideration of isolated intersecting strips ignores the effect of connecting adjacent strips through twisting moments. The favourable effect of the twisting moments on the span bending moments is provided by the twist coefficients νi (i=x, y), where:
The twisting moments affect only the span bending moments.
When the slab supports are not monolithic, such as when coincident free edges exist and no twist reinforcement is provided, then the resulting bending moments on the spans are greater, i.e.:
The equations for the six cases of two-way slabs are specialized according to the support types. Indicatively, coefficients for three aspect ratios are determined:
Type 1 (four simply supported edges)
For ε=1.0: kx=0.500, ky=0.500, νx=0.583, νy=0.583, 100am=4.55 (against 4.87) For ε=3/2: kx=0.835, ky=0.165, νx=0.691, νy=0.691, 100am=9.02 (against 9.27)
For ε=2/3: kx=0.073, ky=0.927, νx=0.863, νy=0.807, 100am=0.98 (against 4.98/1.54=0.98) For ε=1.0: kx=0.286, ky=0.714, νx=0.762,νy=0.665, 100am=3.41 (against 3.34) For ε=3/2: kx=0.669, ky=0.331, νx=0.752, νy=0.651, 100am=7.86 (against 7.73) Type 3 (two opposite fixed edges)
For ε=2/3: kx=0.038, ky=0.962, νx=0.929, νy=0.881, 100am=0.55 (against 2.97/1.54=0.59) For ε=1.0: kx=0.167, ky=0.833, νx=0.861, νy=0.769, 100am=2.25 (against 2.30) For ε=3/2: kx=0.503, ky=0.497, νx=0.814, νy=0.690, 100am=6.40 (against 6.39) Type 4 (two adjacent fixed edges)
For ε=2/3: kx=0.165, ky=0.835, νx=0.826, νy=0.826, 100am=0.85 (against 4.59/1.54=0.91) For ε=1.0: kx=0.500, ky=0.500, νx=0.765, νy=0.765, 100am=2.39 (against 2.52) For ε=3/2: kx=0.835, ky=0.165, νx=0.826, νy=0.826, 100am=4.31 (against 4.59) Type 5 (three fixed edges)
For ε=2/3: kx=0.090, ky=0.910, νx=0.905, νy=0.888, 100am=0.51 (against 2.9/1.54=0.57) For ε=1.0: kx=0.333, ky=0.667, νx=0.844, νy=0.815, 100am=1.76 (against 1.88) For ε=3/2: kx=0.717, ky=0.283, νx=0.850, νy=0.823, 100am=3.81 (against 4.09) Type 6 (four fixed edges)
For ε=2/3: kx=0.165, ky=0.835, νx=0.897 and νy=0.897, 100am=0.46 (against 2.64/1.54=0.52) For ε=1.0: kx=0.500, ky=0.500, νx=0.861 and νy=0.861, 100am=1.35 (against 1.52) For ε=3/2: kx=0.835, ky=0.165, νx=0.897 and νy=0.897, 100am=2.34 (against 2.64) -
In case of ribbed (Zoellner) slab, moments and deflection curve are calculated approximately by using reduced factor νx, νy e.g. equal to ν'x, ν'y, or even with value 1.0. -
To calculate the deflection the actual moments of inertia I of the ribbed slab is used, obtained by multiplying the corresponding table value with the reduction factor Ι/(1.0· h3/12)<1.0.
CZERNY's elasticity method
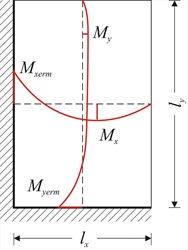 Figure 4.6.2.2
Figure 4.6.2.2 Figure 4.6.2.2 The coefficients used for the determination of spans and supports bending moments result from the tables of §4.6.1.2, depending on the aspect ratio ε = lx / ly (wherein lx is the shortest dimension) and the type of support. Thus:
-
Czerny method, the bending moments and the shear forces are expressed as a function of the shortest distance lx, whereas in Marcus method, the bending moment in each direction is a function of the respective dimension. -
Slab tables usually referred to aspect ratios ly/lx≥1. When ly/lx<1, slabs are considered rotated by 90 ο. -
Twisting moments Mxy are also provided by certain tables (when proper conditions met), as well as shear forces due to bending with or without twisting moments at the edges.
|