Comparison of multistorey frame and dual systems The behaviour of the most common structural systems will be now examined. The structural system comprising only columns is called a frame system, while the one comprising both columns and walls is called a dual system. The comparison of the two systems will be performed by means of examples. The structures under consideration are those used in the two previous paragraphs while the corresponding number of storeys is 4, 8 and 15. Two main quantities are compared, an actual one and an idealised one. The displacement of each level is the actual quantity and the equivalent column cross-section of each storey is the idealised one. The term equivalent column defines a theoretical column which develops a displacement equal to that developed by all storey columns. Infinite types of such idealised equivalent columns could be considered, however the fixed-ended one with 300 mm width is selected here. Alternatively, the rectangular fixed-ended column could be considered as equivalent. The three examples under consideration in both frame and dual versions are included in the related software. The modelling accounts for the elasticstiffnesses (Beam & Column Inertia Factor=1), the rigid bodies effect (Rigid Body=1) and the shear effect ( Shear Effect=1). Stiffness parameter values and values for seismic forces are listed below.  Figure 5.3.3-1
Figure 5.3.3-1 Figure 5.3.3-1 | 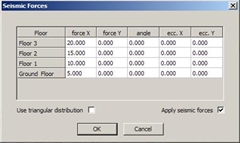 Figure 5.3.3-2
Figure 5.3.3-2 Figure 5.3.3-2 | The results derived from the software analysis are listed in the following tables and figures. Four-storey structures (frame and dual type) under the same seismic loading
| | | Frame Structural System (project <B_533a>) | | Storey | Force
H | Shear
force V | Displacement
δtotal | Displacement
δrelative | Σ(K) x 106 | Equivalent
rectangular column | Equivalent
column with
b=300 | | | kN | kN | mm | mm | N/m | mm | mm | | 0 | 5 | 50 | 0.801 | 0.801 | 62 | 483 | 569 | | 1 | 10 | 45 | 1.766 | 0.965 | 47 | 449 | 517 | | 2 | 15 | 35 | 2.532 | 0.766 | 46 | 447 | 513 | | 3 | 20 | 20 | 2.983 | 0.451 | 44 | 442 | 505 |
| | | Dual Structural System (project <B_533b>) | | Storey | Force
H | Shear
force V | Displacement
δtotal | Displacement
δrelative | Σ(K) x 106 | Equivalent
rectangular column | Equivalent
column with
b=300 | | | kN | kN | mm | mm | N/m | mm | mm | | 0 | 5 | 50 | 0.117 | 0.117 | 427 | 801 | 1169 | | 1 | 10 | 45 | 0.341 | 0.224 | 201 | 655 | 872 | | 2 | 15 | 35 | 0.580 | 0.239 | 146 | 603 | 775 | | 3 | 20 | 20 | 0.792 | 0.212 | 94 | 537 | 660 | Eight-storey structures (frame and dual type) under the same seismic loading
| | | Frame Structural System (project <B_533c>) | | Storey | Force H | Shear
force V | Displacement
δtotal | Displacement δrelative | Σ(K) x 106 | Equivalent
rectangular column | Equivalent
column with
b=300 | | | | | | | | | | | kN | kN | mm | mm | N/m | mm | mm | | 0 | 5 | 180 | 2.941 | 2.94 | 61 | 480 | 566 | | 1 | 10 | 175 | 6.780 | 3.85 | 45 | 444 | 509 | | 2 | 15 | 165 | 10.538 | 3.74 | 44 | 442 | 505 | | 3 | 20 | 150 | 13.991 | 3.45 | 43 | 439 | 501 | | 4 | 25 | 130 | 17.031 | 3.04 | 43 | 439 | 501 | | 5 | 30 | 105 | 19.539 | 2.51 | 42 | 437 | 497 | | 6 | 35 | 75 | 21.397 | 1.86 | 40 | 431 | 489 | | 7 | 40 | 40 | 22.511 | 1.11 | 36 | 420 | 471 |
| | | Dual Structural System (project <B_533d>) | | Storey | Force H | Shear
force V | Displacement
δtotal | Displacement δrelative | Σ(K) x 106 | Equivalent
rectangular column | Equivalent
column with
b=300 | | | | | | | | | | | kN | kN | mm | mm | N/m | mm | mm | | 0 | 5 | 180 | 0.488 | 0.49 | 367 | 769 | 1100 | | 1 | 10 | 175 | 1.511 | 1.02 | 172 | 629 | 823 | | 2 | 15 | 165 | 2.760 | 1.25 | 132 | 587 | 747 | | 3 | 20 | 150 | 4.053 | 1.29 | 116 | 567 | 712 | | 4 | 25 | 130 | 5.280 | 1.23 | 106 | 554 | 689 | | 5 | 30 | 105 | 6.374 | 1.09 | 96 | 540 | 665 | | 6 | 35 | 75 | 7.311 | 0.93 | 81 | 517 | 626 | | 7 | 40 | 40 | 8.079 | 0.78 | 51 | 459 | 532 | Fifteen-storey structures (frame and dual type) under the same seismic loading
| | | Frame Structural System (project <B_533e>) | | Storey | Force H | Shear force V | Displacement
δtotal | Displacement
δrelative | Σ(K) x 106 | Equivalent
rectangular
column | Equivalent
column with
b=300 | | | kN | kN | mm | mm | N/m | mm | mm | | 0 | 5 | 600 | 9.939 | 9.9 | 60 | 478 | 563 | | 1 | 10 | 595 | 23.384 | 13.4 | 44 | 442 | 505 | | 2 | 15 | 585 | 37.166 | 13.8 | 42 | 437 | 497 | | 3 | 20 | 570 | 50.950 | 13.8 | 41 | 434 | 493 | | 4 | 25 | 550 | 64.571 | 13.6 | 40 | 431 | 489 | | 5 | 30 | 525 | 77.880 | 13.3 | 39 | 428 | 484 | | 6 | 35 | 495 | 90.728 | 12.8 | 39 | 428 | 484 | | 7 | 40 | 460 | 102.971 | 12.2 | 38 | 426 | 480 | | 8 | 45 | 420 | 114.467 | 11.5 | 37 | 423 | 476 | | 9 | 50 | 375 | 125.075 | 10.6 | 35 | 417 | 467 | | 10 | 55 | 325 | 134.658 | 9.6 | 34 | 414 | 462 | | 11 | 60 | 270 | 143.085 | 8.4 | 32 | 407 | 452 | | 12 | 65 | 210 | 150.226 | 7.1 | 29 | 397 | 437 | | 13 | 70 | 145 | 155.958 | 5.7 | 25 | 382 | 416 | | 14 | 75 | 75 | 160.198 | 4.2 | 18 | 352 | 371 | | | 600 | 6200 | | | | | |
| | | Dual Structural System (project <B_533f>) | | Storey | Force H | Shear force V | Displacement
δtotal | Displacement
δrelative | Σ(K) x 106 | Equivalent
rectangular
column | Equivalent
column with
b=300 | | | kN | kN | mm | mm | N/m | mm | mm | | 0 | 5 | 600 | 1.797 | 1.8 | 333 | 749 | 1059 | | 1 | 10 | 595 | 5.737 | 3.9 | 153 | 610 | 788 | | 2 | 15 | 585 | 10.851 | 5.1 | 115 | 566 | 710 | | 3 | 20 | 570 | 16.605 | 5.8 | 98 | 543 | 670 | | 4 | 25 | 550 | 22.687 | 6.1 | 90 | 531 | 650 | | 5 | 30 | 525 | 28.899 | 6.2 | 85 | 523 | 637 | | 6 | 35 | 495 | 35.101 | 6.2 | 80 | 515 | 623 | | 7 | 40 | 460 | 41.186 | 6.1 | 75 | 507 | 609 | | 8 | 45 | 420 | 47.064 | 5.9 | 71 | 500 | 598 | | 9 | 50 | 375 | 52.659 | 5.6 | 67 | 492 | 585 | | 10 | 55 | 325 | 57.904 | 5.2 | 63 | 485 | 573 | | 11 | 60 | 270 | 62.750 | 4.8 | 56 | 470 | 550 | | 12 | 65 | 210 | 67.165 | 4.4 | 48 | 452 | 521 | | 13 | 70 | 145 | 71.160 | 4.0 | 36 | 420 | 471 | | 14 | 75 | 75 | 74.816 | 3.7 | 20 | 361 | 385 | | | 600 | 6200 | | | | | |
The storey displacements in case of beams having infinite moment of inertia [*] NoteIn practice very high moment of inertia only approaches infinite value. High moment of inertia is met in cases of beams with large height e.g. 800 mm or even larger. However such cases oppose the capacity design rule, described in volume A’ §1.4.2. , using the values of §5.1.1 are: NoteIn practice very high moment of inertia only approaches infinite value. High moment of inertia is met in cases of beams with large height e.g. 800 mm or even larger. However such cases oppose the capacity design rule, described in volume A’ §1.4.2. , using the values of §5.1.1 are: Frame type structure:
δtot= Σ(V)storeys/ Σ(K)storey=6200kN/(3·K400/400)=(6200·103Ν)/(3 ·29.82·106N/m)=69 mm compared to 160 mm of the actual storey. Dual type structure:
δtot= Σ(V)storeys/ Σ(K)storey=6200kN/(2·K400/400+1·K 2000/300)= =(6200·103Ν)/[(2·29.82+1410.75)·106N/m)=4 mm only, compared to 75 mm of the actual storey. Four-storey structures under the same seismic loading 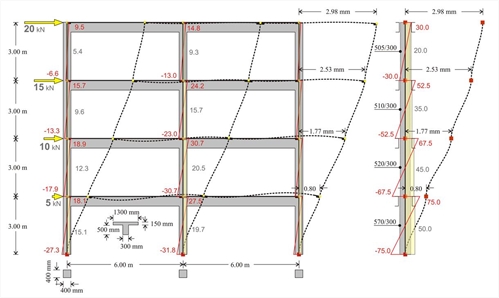 Figure 5.3.3-3: FRAME type structure comprising three columns with cross-section 400/400 and equivalent structure of one fixed-ended column per storey
Figure 5.3.3-3: FRAME type structure comprising three columns with cross-section 400/400 and equivalent structure of one fixed-ended column per storey Figure 5.3.3-3: FRAME type structure comprising three columns with cross-section 400/400 and equivalent structure of one fixed-ended column per storey 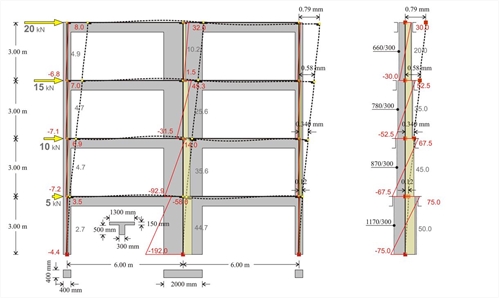 Figure 5.3.3-4: DUAL type structure comprising one wall with a cross-section of 2000/300 and two columns a with a cross-section of 400/400 and Equivalent structure of one fixed-ended column per storey
Figure 5.3.3-4: DUAL type structure comprising one wall with a cross-section of 2000/300 and two columns a with a cross-section of 400/400 and Equivalent structure of one fixed-ended column per storey Figure 5.3.3-4: DUAL type structure comprising one wall with a cross-section of 2000/300 and two columns a with a cross-section of 400/400 and Equivalent structure of one fixed-ended column per storey
The interstorey stiffness variation of the frame type structure is small (equivalent cross-section 570/300 at level 1 and 505/300 at level 4), compared to that corresponding to dual type structure, which is significant (1170/300 and 660/300 respectively). Eight-storey frame type structure under triangular seismic loading  Figure 5.3.3-5: FRAME type structure comprising three column with cross-section 400/400 and equivalent structure of one fixed-ended column per storey
Figure 5.3.3-5: FRAME type structure comprising three column with cross-section 400/400 and equivalent structure of one fixed-ended column per storey Figure 5.3.3-5: FRAME type structure comprising three column with cross-section 400/400 and equivalent structure of one fixed-ended column per storey
- In all types of structures, frame or dual, the sum of column shear forces of a storey is equal to the sum of the seismic forces of all the above storeys. Indicatively, for the first storey the sum is 54.3+71.4+54.3=180, while for the last 10.7+18.6+10.7=40. The middle column of the first storey carries the 71.4/180=40% of the total shear force, while each of the end columns carries 30%. In the last storey the middle column carries the 18.6/40=46%, while each of the end columns carries 27%.
- In both frame and dual systems, for each column Mo-Mu=V·h, where Mo is the moment at the top, Mu is the moment at the base, V is the shear force and h is the height of the column. For instance, for the middle column of the previous structure 98.7-(-115.6)=71.4·3.0 (214.3≈214.2).
Eight-storey dual type structure under triangular seismic loading  Figure 5.3.3-6: DUAL type structure comprising two columns and one wall with cross-sections 400/400 and 2000/300 respectively and equivalent structure of one fixed-ended column per storey
Figure 5.3.3-6: DUAL type structure comprising two columns and one wall with cross-sections 400/400 and 2000/300 respectively and equivalent structure of one fixed-ended column per storey Figure 5.3.3-6: DUAL type structure comprising two columns and one wall with cross-sections 400/400 and 2000/300 respectively and equivalent structure of one fixed-ended column per storey
- In the first storey, the sum is 10.6+158.9+10.6=180. The wall carries 158.9/180=88% of the total shear force, while each column carries 11%. In the last storey, the sum is13.8+12.5+13.8=40. The wall carries 12.5/40=32% of the total shear force, while each column 34%. It is concluded that the wall has a favourable effect on the first storey columns, in contrast to that corresponding to the last storey.
- The expression Mo-Mu=V·h, applies for both columns and wall. Indicatively, for the first storey wall -309.9-(-786.4)=158.9·3.0 (476.5≈476.7), while for that of the last storey 89.8-52.3=12.5·3.0 (37.5=37.5).
- The maximum displacement of the dual type structure is equal to 8.08 mm, i.e. almost three times smaller than the one corresponding to the frame type structure (22.51 mm).
Fifteen-storey frame type structure under triangular seismic loading  Figure 5.3.3-7: FRAME type structure comprising three columns with cross-section 400/400 and equivalent structure of one fixed-ended column per storey
Figure 5.3.3-7: FRAME type structure comprising three columns with cross-section 400/400 and equivalent structure of one fixed-ended column per storey Figure 5.3.3-7: FRAME type structure comprising three columns with cross-section 400/400 and equivalent structure of one fixed-ended column per storey
It should be emphasised that in all previous examples, the comparison of the two structural systems is important rather than the absolute quantities, which after all derive from specific values of the seismic forces. These values have been selected arbitrarily, yet satisfying the triangular distribution rule. Fifteen-storey dual type structure under triangular seismic loading 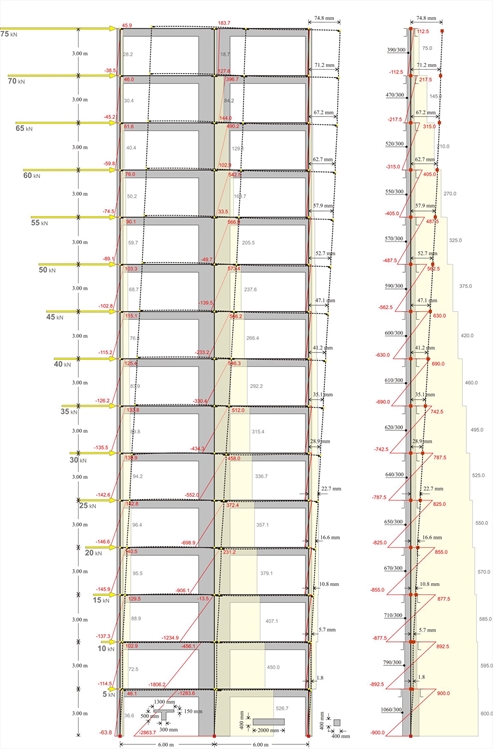 Figure 5.3.3-8: DUAL type structure comprising one wall with a cross section of 2000/300 and two columns with a cross section of 400/400 with cross-sections 400/400 and 2000/300 respectively and equivalent structure of one fixed-ended column per storey
Figure 5.3.3-8: DUAL type structure comprising one wall with a cross section of 2000/300 and two columns with a cross section of 400/400 with cross-sections 400/400 and 2000/300 respectively and equivalent structure of one fixed-ended column per storey Figure 5.3.3-8: DUAL type structure comprising one wall with a cross section of 2000/300 and two columns with a cross section of 400/400 with cross-sections 400/400 and 2000/300 respectively and equivalent structure of one fixed-ended column per storey
The maximum displacement of the frame type structure is equal to 160 mm, i.e. almost twice of that corresponding to the dual type structure (75 mm). Comparative table of Frame and Dual structural systems
| | | | | | | | | | | Need for wide seismic joint between buildings in frame systems. | Earthquake resistance of brick walls | | | EC8 prohibits in general using brittle walls e.g. brick walls for High Ductility Class (DCH) (see§6.1.5.4). | Fluctuation of interstorey relative displacements and stiffnesses | | | In dual systems, walls develop a favourable behaviour in lower while frames develop a favourable behaviour in upper storeys. To this end, the coexistence of both frames and walls in a structure is necessary (dual system). | | | | | Walls should be founded on foundation beams of high stiffness. The more efficient foundation for walls way is on the basement walls ensuring fixity at their base. | | | | | The shear effect should be taken into account in the design of dual systems in contrast to the design of frame systems where it can be omitted. | | | | | The rigid bodies effect should be taken into account in the design of dual systems while in the design of frame systems it can be omitted. |
The behaviour of dual systems is more favourable than frame systems under seismic actions. |